题目内容
四边形ABCD中,解析:∵![]() +
+![]() +
+![]() +
+![]() =0,
=0,
∴a+b+c+d=0.
∴(a+b)=-(c+d),两边平方,得a2+2a·b+b2=c2+2c·d+d2.
∵a·b=c·d,
∴|a|2+|b|2=|c|2+|d|2. ①
同理可得|a|2+|d|2=|c|2+|b|2. ②
①+②得2|a|2=2|c|2![]() |a|=|c|,
|a|=|c|,
①-②得2|b|2=2|d|2![]() |b|=|d|,
|b|=|d|,
即|![]() |=
|=![]() |
|![]() |,|
|,|![]() |=|
|=|![]() |.
|.
∴四边形ABCD是平行四边形.
∴![]() =-
=-![]() ,即a=-c.
,即a=-c.
又a·b=b·c,
∴a·b=b(-a),即a·b=0.
∴a⊥b,即![]() ⊥
⊥![]() .
.
故四边形ABCD是矩形.

练习册系列答案
相关题目
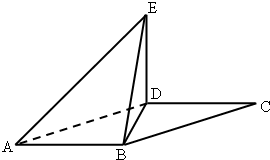 如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4将△CBD沿BD折起到△EBD的位置,使平面EDB⊥平面ABD.
如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4将△CBD沿BD折起到△EBD的位置,使平面EDB⊥平面ABD. (1)已知0<α<
(1)已知0<α<