题目内容
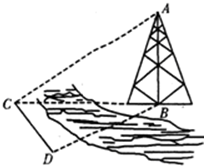如图，测量河对岸的塔高AB时，可以选与塔底B在同一水平面内的两个测点C与D．测得∠BCD=15°，∠BDC=30°，CD=30米，并在点C测得塔顶A的仰角为60°，则塔高AB=分析：先根据三角形的内角和求出∠CBD，再根据正弦定理求得BC，进而在直角三角形ACB中根据∠ACB及BC，进而求得AB．
解答：解：∠CBD=180°-∠BCD-∠BDC=135°，
根据正弦定理
=
，
∴BC=
•sin∠BDC=
×
=15
，
∴AB=tan∠ACB•CB=
×15
=15
，
故答案为15
．
根据正弦定理
| BC |
| sin∠BDC |
| CD |
| sin∠CBD |
∴BC=
| CD |
| sin∠CBD |
| 30 | ||||
|
| 1 |
| 2 |
| 2 |
∴AB=tan∠ACB•CB=
| 3 |
| 2 |
| 6 |
故答案为15
| 6 |
点评：本题主要考查了正弦定理的应用．属基础题．
练习册系列答案
小题狂做系列答案
相关题目
如图，测量河对岸的塔高AB时，可以选与塔底B在同一水平面内的两个测点C与D，测得∠BCD=75°，∠BDC=60°，CD=60米，并在点C测得塔顶A的仰角为60°，则塔高AB=（ ）
如图，测量河对岸的塔高AB时，可以选与塔底B在同一水平面内的两个侧点C与D．现测得∠BCD=α，∠BDC=β，CD=s，并在点C测得塔顶A的仰角为θ，则塔高AB=
如图，测量河对岸的塔高AB时，可以选与塔底B在同一水平面内的两个测点C与D，现测得∠BCD=45°，∠BDC=60°，CD=10m，并在点C测得塔顶A的仰角为45°，则塔高AB=
如图，测量河对岸的塔高AB时可以选与塔底B在同一水平面内的两个测点C与D，测得∠BCD=15°，∠BDC=30°，CD=30，并在点C测得塔顶A的仰角为60°，则塔高AB=（ ）
如图，测量河对岸的塔高AB时，可以选与塔底B在同一水平面内的两个测点C与D．测得∠BDC=30°，CD=30米，并在点C测得塔顶A的仰角为60°，