题目内容
【题目】已知![]() ,函数
,函数![]() ,
,![]() .
.
(1)若![]() 在
在![]() 上单调递增,求正数
上单调递增,求正数![]() 的最大值;
的最大值;
(2)若函数![]() 在
在![]() 内恰有一个零点,求
内恰有一个零点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)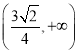
【解析】
(1)求出![]() 的单调递增区间,令
的单调递增区间,令![]() ,得
,得![]() ,可知区间
,可知区间![]()
![]() ,即可求出正数
,即可求出正数![]() 的最大值;(2)令
的最大值;(2)令![]() ,当
,当![]() 时,
时,![]() ,可将问题转化为
,可将问题转化为![]() 在
在![]() 的零点问题,分类讨论即可求出答案.
的零点问题,分类讨论即可求出答案.
解:(1)由![]() ,
,![]()
得![]() ,
,![]() .
.
因为![]() 在
在![]() 上单调递增,
上单调递增,
令![]() ,得
,得![]() 时
时![]() 单调递增,
单调递增,
所以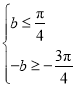 解得
解得![]() ,可得正数
,可得正数![]() 的最大值为
的最大值为![]() .
.
(2)![]()
![]() ,
,
设![]() ,当
,当![]() 时,
时,![]() .它的图形如图所示.
.它的图形如图所示.
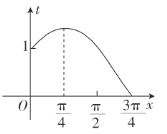
又![]() ,则
,则![]()
![]() ,
,![]() ,令
,令![]() ,
,
则函数![]() 在
在![]() 内恰有一个零点,可知
内恰有一个零点,可知![]() 在
在![]() 内最多一个零点.
内最多一个零点.
①当0为![]() 的零点时,
的零点时,![]() 显然不成立;
显然不成立;
②当![]() 为
为![]() 的零点时,由
的零点时,由![]() ,得
,得![]() ,把
,把![]() 代入
代入![]() 中,
中,
得![]() ,解得
,解得![]() ,
,![]() ,不符合题意.
,不符合题意.
③当零点在区间![]() 时,若
时,若![]() ,得
,得![]() ,此时零点为1,即
,此时零点为1,即![]() ,由
,由![]() 的图象可知不符合题意;
的图象可知不符合题意;
若![]() ,即
,即![]() ,设
,设![]() 的两根分别为
的两根分别为![]() ,
,![]() ,由
,由![]() ,且抛物线的对称轴为
,且抛物线的对称轴为![]() ,则两根同时为正,要使
,则两根同时为正,要使![]() 在
在![]() 内恰有一个零点,则一个根在
内恰有一个零点,则一个根在![]() 内,另一个根在
内,另一个根在![]() 内,
内,
所以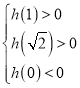 解得
解得![]() .
.
综上,![]() 的取值范围为
的取值范围为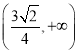 .
.

 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案【题目】某企业生产一种产品,质量测试分为:指标不小于![]() 为一等品;指标不小于
为一等品;指标不小于![]() 且小于
且小于![]() 为二等品;指标小于
为二等品;指标小于![]() 为三等品。其中每件一等品可盈利
为三等品。其中每件一等品可盈利![]() 元,每件二等品可盈利
元,每件二等品可盈利![]() 元,每件三等品亏损
元,每件三等品亏损![]() 元。现对学徒甲和正式工人乙生产的产品各
元。现对学徒甲和正式工人乙生产的产品各![]() 件的检测结果统计如下:
件的检测结果统计如下:
测试指标 |
|
|
|
|
|
|
甲 |
|
|
|
|
|
|
乙 |
|
|
|
|
|
|
根据上表统计得到甲、乙生产产品等级的频率分别估计为他们生产产品等级的概率。求:
(1)乙生产一件产品,盈利不小于![]() 元的概率;
元的概率;
(2)若甲、乙一天生产产品分别为![]() 件和
件和![]() 件,估计甲、乙两人一天共为企业创收多少元?
件,估计甲、乙两人一天共为企业创收多少元?
(3)从甲测试指标为![]() 与乙测试指标为
与乙测试指标为![]() 共
共![]() 件产品中选取
件产品中选取![]() 件,求两件产品的测试指标差的绝对值大于
件,求两件产品的测试指标差的绝对值大于![]() 的概率.
的概率.
【题目】某学校为了了解该校学生对于某项运动的爱好是否与性别有关,通过随机抽查110名学生,得到如下![]() 的列联表:
的列联表:
喜欢该项运动 | 不喜欢该项运动 | 总计 | |
男 | 40 | 20 | 60 |
女 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由公式 ,算得
,算得![]()
附表:
| 0.025 | 0.01 | 0.005 |
| 5.024 | 6.635 | 7.879 |
参照附表,以下结论正确的是( )
A. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
B. 在犯错语的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
C. 有99%以上的把握认为“爱好该项运动与性别无关”
D. 有99%以上的把握认为“爱好该项运动与性别有关”