题目内容
在四棱柱ABCD—A1B1C1D1中,底面是边长为
证明:把四棱柱如图放置在空间直角坐标系中,则各点坐标为A(![]() ,0,0),C(0,
,0,0),C(0,![]() ,0),B1(
,0),B1(![]() ,
,![]() ,
,![]() ),D1(0,0,
),D1(0,0,![]() ),E(
),E(![]() ),F(
),F(![]() ).
).
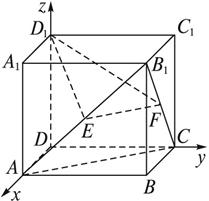
假设平面AB1C的法向量为n1=(1,λ1,μ1),则n1应垂直于![]() .而
.而![]()
∴![]()
∴λ1=1,μ1=-![]() .∴n1=(1,1,-
.∴n1=(1,1,-![]() ).
).
再假设平面D1EF的法向量为n2=(1,λ2,μ2),则n2应垂直于![]() 、
、![]() ,而
,而![]() =(
=(![]() ),
),![]()
∴![]()
∴λ2=1,μ2=![]() .
.
∴n2=(1,1,![]() ).
).
由于n1·n2=1+1-![]() =1+1-2=0,
=1+1-2=0,
∴n1⊥n2.因此平面D1EF⊥平面AB1C.

练习册系列答案
相关题目
顶点在同一球面上的正四棱柱ABCD-A′B′C′D′中,AB=1,AA′=
,则A、C两点间的球面距离为( )
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是正方形,侧棱与底面垂直,E,F分别是AB1,BC1的中点,则以下结论中不成立的是( )
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是正方形,侧棱与底面垂直,E,F分别是AB1,BC1的中点,则以下结论中不成立的是( )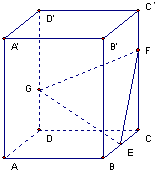 如图,正四棱柱ABCD-A′B′C′D′中,底面边长为2,侧棱长为3,E为BC的中点,FG分别为CC′、DD′上的点,且CF=2GD=2.求:
如图,正四棱柱ABCD-A′B′C′D′中,底面边长为2,侧棱长为3,E为BC的中点,FG分别为CC′、DD′上的点,且CF=2GD=2.求: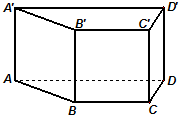 在高为1的直四棱柱ABCD-A'B'C'D'中,底面ABCD是等腰梯形,AB=BC=CD=1,AD=2.
在高为1的直四棱柱ABCD-A'B'C'D'中,底面ABCD是等腰梯形,AB=BC=CD=1,AD=2.