题目内容
已知各个面都是平行四边形的四棱柱ABCD-A′B′C′D′
（1）化简
+
+
，并在图形中标出其结果；
（2）设M是底面ABCD的中心，N是侧面BCC′B′的对角线BC′上的点，且BN：NC′=3：1，设
=α
+β
+γ
，试求α，β，γ的值．
（1）化简
| 1 |
| 2 |
| AA′ |
| BC |
| 2 |
| 3 |
| AB |
（2）设M是底面ABCD的中心，N是侧面BCC′B′的对角线BC′上的点，且BN：NC′=3：1，设
| MN |
| AB |
| AD |
| AA′ |
分析：（1）如图所示，取线段AA′中点E，则
=
，
=
=
，取D′F=
D′C′，由AB=D′C′，可得
=
=
．即可得出．
（2）利用三角形法则及其平行四边形法则和向量共线定理、向量线段即可得出．
| EA′ |
| 1 |
| 2 |
| AA′ |
| BC |
| AD |
| A′D′ |
| 2 |
| 3 |
| 2 |
| 3 |
| AB |
| 2 |
| 3 |
| D′C′ |
| D′F |
（2）利用三角形法则及其平行四边形法则和向量共线定理、向量线段即可得出．
解答：解：（1）如图所示，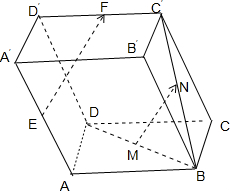
取线段AA′中点E，则
=
，
=
=
，取D′F=
D′C′，∵AB=D′C′，
∴
=
=
．
则
+
+
=
+
+
=
．
（2）∵
=
+
=
+
=
(
+
)+
(
+
)=
+
+
=α
+β
+γ
，
∴α=
，β=
，γ=
．
取线段AA′中点E，则| EA′ |
| 1 |
| 2 |
| AA′ |
| BC |
| AD |
| A′D′ |
| 2 |
| 3 |
∴
| 2 |
| 3 |
| AB |
| 2 |
| 3 |
| D′C′ |
| D′F |
则
| 1 |
| 2 |
| AA′ |
| BC |
| 2 |
| 3 |
| AB |
| EA′ |
| A′D′ |
| D′F |
| EF |
（2）∵
| MN |
| MB |
| BN |
| 1 |
| 2 |
| DB |
| 3 |
| 4 |
| BC′ |
| 1 |
| 2 |
| DA |
| AB |
| 3 |
| 4 |
| BC |
| CC′ |
| 1 |
| 2 |
| AB |
| 1 |
| 4 |
| AD |
| 3 |
| 4 |
| AA′ |
| AB |
| AD |
| AA′ |
∴α=
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
点评：熟练掌握三角形法则及其平行四边形法则和向量共线定理、向量线段等是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
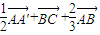，并在图形中标出其结果；
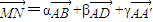，试求α，β，γ的值．