题目内容
设函数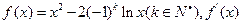 表示f(x)导函数。
表示f(x)导函数。
(I)求函数一份(x))的单调递增区间;
(Ⅱ)当k为偶数时,数列{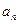 }满足
}满足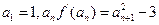 .证明:数列{
.证明:数列{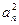 }中
}中
不存在成等差数列的三项;
(Ⅲ)当后为奇数时,证明:对任意正整数,n都有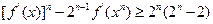 成立.
成立.
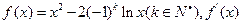 表示f(x)导函数。
表示f(x)导函数。(I)求函数一份(x))的单调递增区间;
(Ⅱ)当k为偶数时,数列{
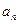 }满足
}满足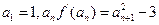 .证明:数列{
.证明:数列{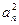 }中
}中不存在成等差数列的三项;
(Ⅲ)当后为奇数时,证明:对任意正整数,n都有
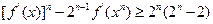 成立.
成立.(1)当k为奇数时,f(x)的单调递增区间为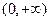 ,当k为偶数时f(x)的单调递增区间为
,当k为偶数时f(x)的单调递增区间为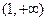 (2)见解析(3)见解析
(2)见解析(3)见解析
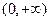 ,当k为偶数时f(x)的单调递增区间为
,当k为偶数时f(x)的单调递增区间为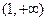 (2)见解析(3)见解析
(2)见解析(3)见解析(Ⅰ)函数的定义域为(0,+∞)
又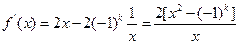
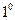 当k为奇数时,
当k为奇数时,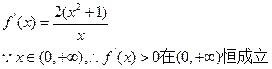
即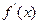 的单调递增区间为
的单调递增区间为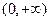
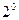 当k为偶函数时,
当k为偶函数时,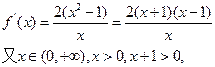
由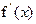 >0,得x-1>0,∴x>1,即f(x)的单调递增区间为
>0,得x-1>0,∴x>1,即f(x)的单调递增区间为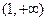 ,
,
综上所述:当k为奇数时,f(x)的单调递增区间为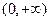 ,当k为偶数时f(x)的单调递增区间为
,当k为偶数时f(x)的单调递增区间为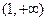
(Ⅱ)当k为偶数时,由(Ⅰ)知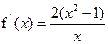
所以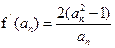
根据题设条件有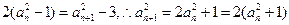
∴{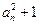 }是以2为公式的比例数列
}是以2为公式的比例数列
假设数列{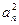 }中存在三项
}中存在三项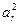 ,
,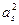 ,
,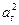 ,成等差数列
,成等差数列
不妨设r<s<t,则2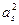 =
=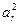 +
+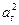
即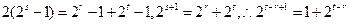
又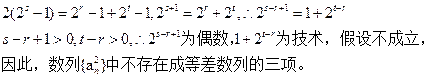
(Ⅲ)当k为奇数时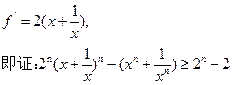
方法二:(数学归纳发)
当n=1是,左边=0,右边=0,显然不等式成立
设n=k+1时: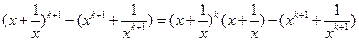
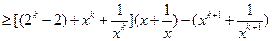
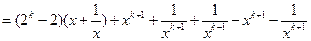
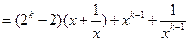
又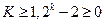
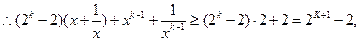
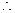 n=k+1时结论成立。
n=k+1时结论成立。
综上,对一切正整数n结论成立。
又
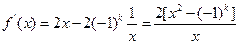
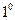 当k为奇数时,
当k为奇数时,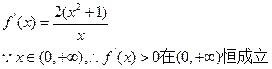
即
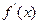 的单调递增区间为
的单调递增区间为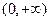
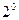 当k为偶函数时,
当k为偶函数时,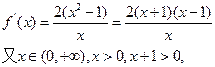
由
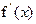 >0,得x-1>0,∴x>1,即f(x)的单调递增区间为
>0,得x-1>0,∴x>1,即f(x)的单调递增区间为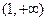 ,
,综上所述:当k为奇数时,f(x)的单调递增区间为
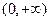 ,当k为偶数时f(x)的单调递增区间为
,当k为偶数时f(x)的单调递增区间为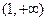
(Ⅱ)当k为偶数时,由(Ⅰ)知
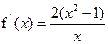
所以
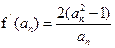
根据题设条件有
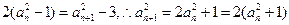
∴{
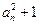 }是以2为公式的比例数列
}是以2为公式的比例数列 假设数列{
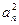 }中存在三项
}中存在三项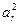 ,
,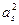 ,
,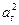 ,成等差数列
,成等差数列不妨设r<s<t,则2
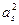 =
=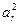 +
+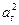
即
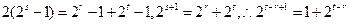
又
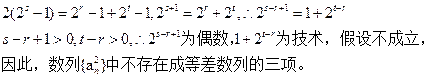
(Ⅲ)当k为奇数时
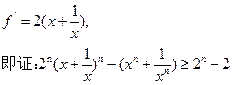
方法二:(数学归纳发)
当n=1是,左边=0,右边=0,显然不等式成立
设n=k+1时:
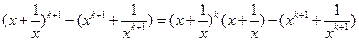
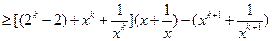
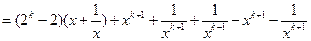
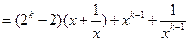
又
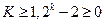
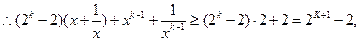
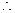 n=k+1时结论成立。
n=k+1时结论成立。综上,对一切正整数n结论成立。

练习册系列答案
相关题目
 为
为 ,射线
,射线 为
为 ,动点
,动点 在
在 的内部,
的内部, 于
于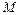 ,
, 于
于 ,四边形
,四边形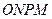 的面积恰为
的面积恰为 .
. 的纵坐标
的纵坐标 是横坐标
是横坐标 的函数,求这个函数
的函数,求这个函数 的解析式;
的解析式;
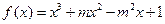
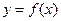 的切线,求此直线方程.
的切线,求此直线方程.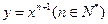 在点(1,1)处的切线与x轴的交点的横坐标为
在点(1,1)处的切线与x轴的交点的横坐标为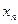 ,
,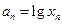 ,则
,则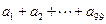 的值为 .
的值为 .  万元的一条流水线,要提高该流水线的生产能力,就要对其进行技术改造,从而提高产品附加值,改造需要投入,假设附加值
万元的一条流水线,要提高该流水线的生产能力,就要对其进行技术改造,从而提高产品附加值,改造需要投入,假设附加值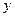 万元与技术改造投入
万元与技术改造投入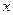 万元之间的关系满足:①
万元之间的关系满足:① 和
和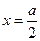 时,
时, ;③
;③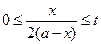 ,其中
,其中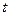 为常数,且
为常数,且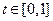 。
。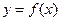 ,求
,求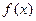 表达式,并求
表达式,并求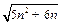 ,汛期共计约40天,当前水库水位为220(标高),而水库警戒水位是400(标高),水库共有水闸15个,每开启一个泄洪,一天可使水位下降4(标高).
,汛期共计约40天,当前水库水位为220(标高),而水库警戒水位是400(标高),水库共有水闸15个,每开启一个泄洪,一天可使水位下降4(标高).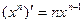 ,
,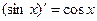 ,
,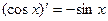 ,是否可判断,可导的奇函数的导函数是偶函数,可导的偶函数的导函数是奇函数。
,是否可判断,可导的奇函数的导函数是偶函数,可导的偶函数的导函数是奇函数。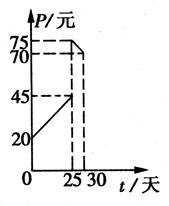
 10
10