题目内容
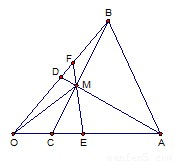
如图,在△ABO中,D、C分别在AO,BO边上,AC,BD交于点M,且AM•MC=BM•MD.(I)证明:∠1=∠2;
(II)证明:A、B、C、D四点共圆.
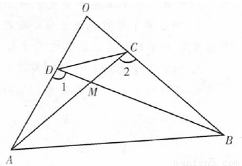
【答案】分析:(I)由已知中AM•MC=BM•MD,根据相似三角形判定定理可得△AMD∽△BMC,进而可由对应角相等得到答案.
(II)由(I)中结论,类比可得,∠DAC=∠DBC,同理可证:∠BAC=∠BDC,∠ACD=∠ABD,进而根据四边形内角和为360°,得到四边形对解互补,进而得到A、B、C、D四点共圆.
解答: 证明:(I)∵AM•MC=BM•MD.
证明:(I)∵AM•MC=BM•MD.
∴ =
= ,又∵∠AMD=∠BMC
,又∵∠AMD=∠BMC
∴△AMD∽△BMC
∴∠1=∠2;
(II)由(I)知,∠DAC=∠DBC
同理可证:∠BAC=∠BDC,∠ACD=∠ABD
∵∠1+∠2+∠DAC+∠DBC+∠BAC+∠BDC+∠ACD+∠ABD=360°
∴∠2+∠DAC+∠BAC+∠ACD=180°
∴A、B、C、D四点共圆
点评:本题考查的知识点是相似三角形的判定与性质,圆内接四边形的判定,熟练掌握相关定理是解答的关键.
(II)由(I)中结论,类比可得,∠DAC=∠DBC,同理可证:∠BAC=∠BDC,∠ACD=∠ABD,进而根据四边形内角和为360°,得到四边形对解互补,进而得到A、B、C、D四点共圆.
解答:
 证明:(I)∵AM•MC=BM•MD.
证明:(I)∵AM•MC=BM•MD.∴
 =
= ,又∵∠AMD=∠BMC
,又∵∠AMD=∠BMC∴△AMD∽△BMC
∴∠1=∠2;
(II)由(I)知,∠DAC=∠DBC
同理可证:∠BAC=∠BDC,∠ACD=∠ABD
∵∠1+∠2+∠DAC+∠DBC+∠BAC+∠BDC+∠ACD+∠ABD=360°
∴∠2+∠DAC+∠BAC+∠ACD=180°
∴A、B、C、D四点共圆
点评:本题考查的知识点是相似三角形的判定与性质,圆内接四边形的判定,熟练掌握相关定理是解答的关键.

练习册系列答案
相关题目
 如图,在△ABO中,D、C分别在AO,BO边上,AC,BD交于点M,且AM•MC=BM•MD.
如图,在△ABO中,D、C分别在AO,BO边上,AC,BD交于点M,且AM•MC=BM•MD.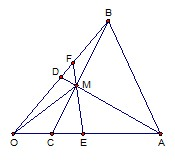 如图,在△ABO中,
如图,在△ABO中,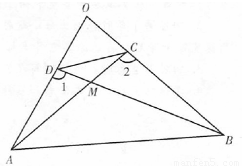
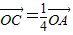 ,
,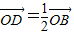 ,AD交BC于M,设
,AD交BC于M,设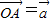 ,
,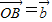 .
.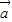 、
、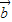 表示
表示 ;
;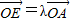 ,
,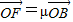 .
. .
.