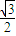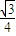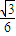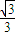题目内容
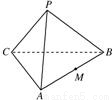
 正四面体PABC中,M为棱AB的中点,则PA与CM所成角的余弦值为( )
正四面体PABC中,M为棱AB的中点,则PA与CM所成角的余弦值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:先通过平移将两条异面直线平移到同一个起点AB的中点M,得到的锐角或直角就是异面直线所成的角,在三角形中再利用余弦定理求出此角即可.
解答: 解:如图,取PB中点N,连接CM、CN、MN.
解:如图,取PB中点N,连接CM、CN、MN.
∠CMN为PA与CM所成的角(或所成角的补角),
设PA=2,则CM=
,MN=1,
CN=
,由余弦定理得:
∴cos∠CMN=
.
故选C.
 解:如图,取PB中点N,连接CM、CN、MN.
解:如图,取PB中点N,连接CM、CN、MN.∠CMN为PA与CM所成的角(或所成角的补角),
设PA=2,则CM=
| 3 |
CN=
| 3 |
∴cos∠CMN=
| ||
| 6 |
故选C.
点评:过空间任意一点引两条直线分别平行于两条异面直线,它们所成的锐角(或直角)就是异面直线所成的角.求两条异面直线所成角的大小一般方法是通过平行移动直线,把异面问题转化为共面问题来解决.

练习册系列答案
相关题目
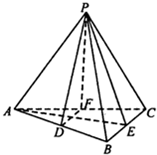 11、在正四面体PABC中,D,E,F分别是棱AB,BC,CA的中点.给出下面四个结论:
11、在正四面体PABC中,D,E,F分别是棱AB,BC,CA的中点.给出下面四个结论: