Question

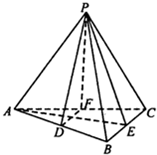11、在正四面体PABC中，D，E，F分别是棱AB，BC，CA的中点．给出下面四个结论：
①BC∥平面PDF；②DF⊥平面PAE；③平面PDF⊥平面ABC；④平面PAE⊥平面ABC，
其中所有不正确的结论的序号是

③

．

Answer 1

分析：正四面体P-ABC即正三棱锥P-ABC，所以其四个面都是正三角形，应该联想到“三线合一”．平面条件为空间问题提供素材．

解答：解：①由DF∥BC可得BC∥平面PDF，①故正确．
②BC⊥PE，BC⊥AE?BC⊥面PAE，
 DF∥BC∴DF⊥平面PAE，②正确
③根据正四面的定义P点在底面的射影是底面△ABC的中心O，
有平面几何知识，O点不在DF上，故③错．
④在②的基础上，DF?面ABC，由面面垂直的判定定理，④正确
故答案为：③．

点评：本小题考查空间中的线面关系，用到了正三角形中“三线合一”，中位线定理等基础知识，考查空间想象能力和思维能力，平面问题空间问题相互转化的能力．