题目内容
设t≠0,点P(t,0)是函数f(x)=x3+ax与g(x)=bx2+c的图象的一个公共点,两函数的图象在点P处有相同的切线。
(1)用t表示a,b,c;
(2)若函数y=f(x)-g(x)在(-1,3)上单调递减,求t的取值范围。
(1)用t表示a,b,c;
(2)若函数y=f(x)-g(x)在(-1,3)上单调递减,求t的取值范围。
解:(1)因为函数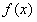 ,
,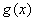 的图象都过点(t,0),
的图象都过点(t,0),
所以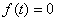 ,
,
即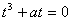
因为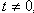
所以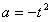
又因为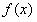 ,
,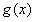 在点(t,0)处有相同的切线,所以
在点(t,0)处有相同的切线,所以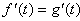
而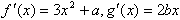
所以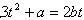
将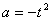 代入上式得
代入上式得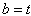
因此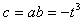
故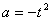 ,
,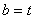 ,
,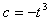 。
。
(2)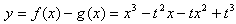
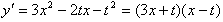
当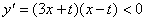 时,函数
时,函数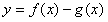 单调递减
单调递减
由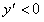 ,若
,若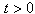
则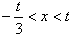
若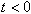 ,则
,则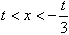
由题意,函数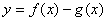 在(-1,3)上单调递减
在(-1,3)上单调递减
则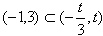 或
或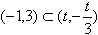
所以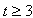 或
或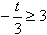
即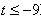 或
或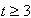
又当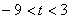 时,函数
时,函数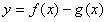 在(-1,3)上单调递减
在(-1,3)上单调递减
所以t的取值范围为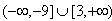 。
。
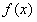 ,
,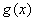 的图象都过点(t,0),
的图象都过点(t,0),所以
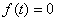 ,
, 即
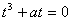
因为
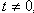
所以
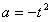
又因为
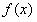 ,
,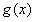 在点(t,0)处有相同的切线,所以
在点(t,0)处有相同的切线,所以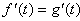
而
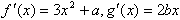
所以
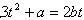
将
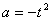 代入上式得
代入上式得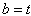
因此
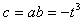
故
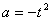 ,
,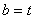 ,
,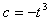 。
。(2)
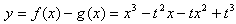
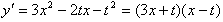
当
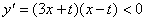 时,函数
时,函数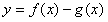 单调递减
单调递减由
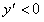 ,若
,若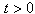
则
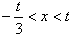
若
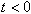 ,则
,则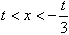
由题意,函数
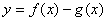 在(-1,3)上单调递减
在(-1,3)上单调递减则
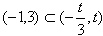 或
或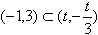
所以
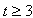 或
或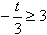
即
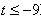 或
或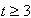
又当
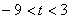 时,函数
时,函数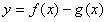 在(-1,3)上单调递减
在(-1,3)上单调递减所以t的取值范围为
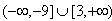 。
。
练习册系列答案
相关题目
 与
与 的图象的一个公共点,两函数的图象在点P处有相同的切线。
的图象的一个公共点,两函数的图象在点P处有相同的切线。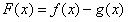 在(-1,3)上单调递减,求t的取值范围。
在(-1,3)上单调递减,求t的取值范围。