题目内容
设t≠0，点P（t，0）是函数
与
的图象的一个公共点，两函数的图象在点P处有相同的切线。
（Ⅰ）用t表示a，b，c；
（Ⅱ）若函数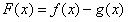
在（-1，3）上单调递减，求t的取值范围。
与的图象的一个公共点，两函数的图象在点P处有相同的切线。（Ⅰ）用t表示a，b，c；
（Ⅱ）若函数
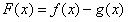在（-1，3）上单调递减，求t的取值范围。 解：（Ⅰ）∵函数
，
的图象都过点（t，0），
∴
，即
，
∵t≠0，
∴
，
∵
∴
，
又∵
，
在点（t，0）处有相同的切线，
∴
而
∴
，
将
代入上式，得b=t，
∴c=ab=-t3，
故
，b=t，c=-t3。
（Ⅱ）
，
∵函数
在在（-1，3）上单调递减，
∴
在（-1，3）上恒成立，
∴
即
，
解得：t≤-9或t≥3，
∴t的取值范围是
，的图象都过点（t，0），∴
，即，∵t≠0，
∴
，∵
∴
，又∵
，在点（t，0）处有相同的切线，∴
而∴
，将
代入上式，得b=t，∴c=ab=-t3，
故
，b=t，c=-t3。（Ⅱ）
， ∵函数
在在（-1，3）上单调递减，∴
在（-1，3）上恒成立，∴
即，解得：t≤-9或t≥3，
∴t的取值范围是
练习册系列答案
相关题目