题目内容
设t≠0,点P(t,0)是函数f(x)=x3+ax与g(x)=bx2+c图象的一个公共点,两函数的图象在点P处有相同的切线,则用t表示c为
c=-t3
c=-t3
.分析:函数f(x),g(x)的图象都过点(t,0),先将(t,0)代入两个函数求出a、b、c的关系,再利用两函数的导数在x=t处的导函数值相同便可求出a、b、c与t的关系.
解答:解:因为函数f(x),g(x)的图象都过点(t,0),
所以f(t)=0,
即t3+at=0.因为t≠0,所以a=-t2.
g(t)=0,即bt2+c=0,所以c=ab.
又因为f(x),g(x)在点(t,0)处有相同的切线,
所以f′(t)=g′(t).
而f′(x)=3x2+a,g′(x)=2bx,所以3t2+a=2bt.
将a=-t2代入上式得b=t.因此c=ab=-t3.
故答案为c=-t3.
所以f(t)=0,
即t3+at=0.因为t≠0,所以a=-t2.
g(t)=0,即bt2+c=0,所以c=ab.
又因为f(x),g(x)在点(t,0)处有相同的切线,
所以f′(t)=g′(t).
而f′(x)=3x2+a,g′(x)=2bx,所以3t2+a=2bt.
将a=-t2代入上式得b=t.因此c=ab=-t3.
故答案为c=-t3.
点评:本题主要考查直线的斜率、导数的几何意义、利用导数研究曲线上某点切线方程等基础知识,考查运算求解能力.属于基础题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 与
与 的图象的一个公共点,两函数的图象在点P处有相同的切线。
的图象的一个公共点,两函数的图象在点P处有相同的切线。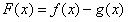 在(-1,3)上单调递减,求t的取值范围。
在(-1,3)上单调递减,求t的取值范围。