题目内容
(本小题满分14分)已知函数 ,其中
,其中 .
.
(1)当 时,求函数
时,求函数 的图象在点
的图象在点 处的切线方程;
处的切线方程;
(2)如果对于任意 ,都有
,都有 ,求
,求 的取值范围.
的取值范围.
(1) ;(2)
;(2) .
.
【解析】
试题分析:本题主要考查导数的运算、利用导数求曲线的切线、利用导数判断函数的单调区间、利用导数求函数的最值等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,先将 代入,得到
代入,得到 解析式,对
解析式,对 求导,得到
求导,得到 为切线的斜率,
为切线的斜率, 为切点的纵坐标,从而利用点斜式得到切线方程;第二问,将
为切点的纵坐标,从而利用点斜式得到切线方程;第二问,将 代入,得到
代入,得到 ,所以将对于任意
,所以将对于任意 ,都有
,都有 转化成了
转化成了 ,构造函数
,构造函数 ,对
,对 求导,通过
求导,通过 判断函数
判断函数 单调递增,从而得
单调递增,从而得 ,即得证.
,即得证.
试题解析:(1)当 时,由已知得
时,由已知得 ,故
,故 , 2分
, 2分
所以 ,又因为
,又因为 ,
,
所以函数 的图象在点
的图象在点 处的切线方程为
处的切线方程为 ,
,
即 ; 5分
; 5分
(2)【解析】
由 ,得
,得 ,又
,又 ,
,
故 . 7分
. 7分
设函数 ,
,
则 . 8分
. 8分
因为 ,
,
所以 ,
, ,
,
所以当 时,
时, , 10分
, 10分
故函数 在
在 上单调递增.
上单调递增.
所以当 时,
时, . 12分
. 12分
因为对于任意 ,都有
,都有 成立,
成立,
所以对于任意 ,都有
,都有 成立.
成立.
所以 . 14分
. 14分
考点:导数的运算、利用导数求曲线的切线、利用导数判断函数的单调区间、利用导数求函数的最值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 满足
满足 ,向量
,向量 .若
.若 ,则实数m的最小值为 .
,则实数m的最小值为 .
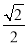 B.
B.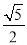 C.
C.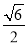 D.
D.
 为
为 的导函数,则
的导函数,则 的图像是( )
的图像是( ) B.
B. C.
C. D.
D.

 B.
B.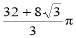
 D.
D.
 ,由下往上的六个点:
,由下往上的六个点: ,
, ,
, ,
, ,
, ,
, 的横、纵坐标分别对应数列
的横、纵坐标分别对应数列 (
( )的前
)的前 项,如下表所示:
项,如下表所示: 
 .
.
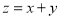 ,其中实数
,其中实数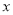 ,
,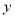 满足
满足 ,则
,则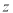 的最大值为( )
的最大值为( )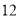 B.
B.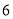 C.
C.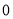 D.
D.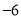
 在点
在点 处的切线方程为 .
处的切线方程为 . 的定义域为__________.
的定义域为__________.