题目内容
求与直线l1:3x+4y-7=0平行,并且与两坐标轴都相交在正半轴所成的三角形面积为24的直线l的方程.
【答案】分析:由题意可得可设l的方程为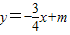 ,m>0,直线l和x轴交点为
,m>0,直线l和x轴交点为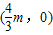 ,由
,由 求出m的值,即可得到所求的直线方程.
求出m的值,即可得到所求的直线方程.
解答:解:直线l1:3x+4y-7=0,化为斜截式: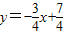 ,所以,l1的斜率为
,所以,l1的斜率为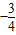 ;
;
∵所求直线l∥l1 ,∴l的斜率也为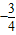 ;∴可设l的方程为
;∴可设l的方程为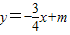 ,…(3分)
,…(3分)
∵l与两坐标轴都相交在正半轴,∴m>0;当y=0时,求得直线l和x轴交点为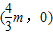 ,
,
由已知l与x轴,y轴所围成的三角形面积为24,所以: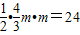 ,…(6分)
,…(6分)
解出:m=±6,由分析m>0,舍去-6,所以,m=6,…(7分)
所以,所求的直线方程为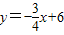 ,即:3x+4y-24=0…(8分)
,即:3x+4y-24=0…(8分)
点评:本题主要考查两直线平行的性质,用点斜式求直线方程的方法,得到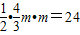 ,是解题的关键,属于基础题.
,是解题的关键,属于基础题.
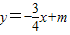 ,m>0,直线l和x轴交点为
,m>0,直线l和x轴交点为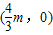 ,由
,由 求出m的值,即可得到所求的直线方程.
求出m的值,即可得到所求的直线方程.解答:解:直线l1:3x+4y-7=0,化为斜截式:
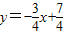 ,所以,l1的斜率为
,所以,l1的斜率为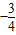 ;
;∵所求直线l∥l1 ,∴l的斜率也为
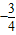 ;∴可设l的方程为
;∴可设l的方程为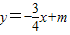 ,…(3分)
,…(3分)∵l与两坐标轴都相交在正半轴,∴m>0;当y=0时,求得直线l和x轴交点为
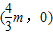 ,
,由已知l与x轴,y轴所围成的三角形面积为24,所以:
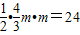 ,…(6分)
,…(6分)解出:m=±6,由分析m>0,舍去-6,所以,m=6,…(7分)
所以,所求的直线方程为
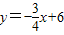 ,即:3x+4y-24=0…(8分)
,即:3x+4y-24=0…(8分)点评:本题主要考查两直线平行的性质,用点斜式求直线方程的方法,得到
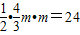 ,是解题的关键,属于基础题.
,是解题的关键,属于基础题. 
练习册系列答案
相关题目