题目内容
已知椭圆
、抛物线
的焦点均在
轴上，的中心和的顶点均为原点
，从每条曲线上取两个点，将其坐标记录于下表中：
| x | 3 |
| 4 |
|
|
|
| 0 |
|
|
(Ⅰ)求，的标准方程；
(Ⅱ)请问是否存在直线
满足条件：①过的焦点
；②与交于不同两点
，
，且满足
？若存在，求出直线的方程；若不存在，说明理由．
解：(Ⅰ)设抛物线：
，则有
，据此验证4个点知
，
在抛物线上，易求：
．
设：
，把点
代入得
，解得，
，
的方程为：
．
综上，的方程为：，的方程为：。
(Ⅱ)假设存在这样的直线，设其方程为
，两交点坐标为
，
由
消去，得
，
①
，②-
，
③
将①②代入③得，
解得
所以假设成立，即存在直线满足条件，且的方程为
或
．-
练习册系列答案
阅读快车系列答案
相关题目
的值域为
，若关于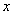
的不等式
的解集为
，则实数
的值为 .
的解集中的整数有且仅有1，2，3
，则
的取值范围 .
分别是双曲线
的左、右焦点，过点
垂直于
两点，若
为锐角三角形，则该双曲线的离心率
的取值范围是
B. 
C. 
D. 
棱长为1，点
，
，且
，有以下四个结论：
①
,②
；③
平面
；④
与
是异面直线.其中正确结论的序号是_____ (注：把你认为正确命题的序号都填上）
B．
C． 
D．
不等式
的解集是R，命题
在区间
上是减函数，若命题“
”为真，则实数
的范围是____.
= ．
的焦点为圆心，且与双曲线
的渐近线相切的圆的方程为（ ）
（B）
（D）