题目内容
如图,已知椭圆C: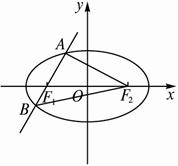
(1)求△ABF2面积的最大值.
(2)求△ABF2面积取得最大值时tan∠F1AF2的值.
解:(1)由![]() ,知F1(-1,0),F2(1,0).?
,知F1(-1,0),F2(1,0).?
设倾角为θ的直线AB(θ≠![]() ):y=k(x+1)和椭圆C交于A(x 1 ,y 1),B(x 2 ,y 2).?
):y=k(x+1)和椭圆C交于A(x 1 ,y 1),B(x 2 ,y 2).?
将y=k(x+1)代入8x 2+9y 2=72中,?
整理得(8+9k2)x 2+18k 2x+9k 2-72=0.?
求得Δ=4×9×64(k2+1),?
|AB|=![]() |x1-x2|=
|x1-x2|=![]() (k=tanθ)?
(k=tanθ)?
△ABF 2面积S=![]() |AB|·|F 1F 2|·sinθ=
|AB|·|F 1F 2|·sinθ=![]() ?
?
=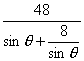 (0<sinθ<1)?
(0<sinθ<1)?
SΔ![]() <
<![]() ,当θ=
,当θ=![]() ,SΔ
,SΔ![]() =
=![]() .?
.?
∴△ABF2面积最大值为![]() .?
.?
(2)在△ABF2面积取最大值时,sinθ=1,则AB⊥x轴.?
∴此时|AF1|=![]() ,而2c=2.
,而2c=2.
在Rt△AF1F2 ,tan∠F1AF2=![]() .
.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 (2013•临沂二模)
(2013•临沂二模) 的左、右焦点分别为
的左、右焦点分别为 ,离心率为
,离心率为 ,点A是椭圆上任一点,
,点A是椭圆上任一点, 的周长为
的周长为 .
. 任作一动直线l交椭圆C于
任作一动直线l交椭圆C于 两点,记
两点,记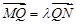 ,若在线段
,若在线段 上取一点R,使得
上取一点R,使得 ,则当直线l转动时,点R在某一定直线上运动,求该定直线的方程.
,则当直线l转动时,点R在某一定直线上运动,求该定直线的方程.
 的上、下顶点分别为A、B,点P在椭圆C上且异于点A、B,直线AP、PB与直线l:y=-2分别交于点M、N.
的上、下顶点分别为A、B,点P在椭圆C上且异于点A、B,直线AP、PB与直线l:y=-2分别交于点M、N.
 如图,已知椭圆C:
如图,已知椭圆C: 的离心率为
的离心率为 ,以椭圆C的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0),设圆T与椭圆C交于点M与点N.
,以椭圆C的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0),设圆T与椭圆C交于点M与点N. 的最小值,并求此时圆T的方程;
的最小值,并求此时圆T的方程; 的长轴AB长为4,离心率
的长轴AB长为4,离心率 ,O为坐标原点,过B的直线l与x轴垂直.P是椭圆上异于A、B的任意一点,PH⊥x轴,H为垂足,延长HP到点Q使得HP=PQ,连接AQ延长交直线l于点M,N为MB的中点.
,O为坐标原点,过B的直线l与x轴垂直.P是椭圆上异于A、B的任意一点,PH⊥x轴,H为垂足,延长HP到点Q使得HP=PQ,连接AQ延长交直线l于点M,N为MB的中点.