题目内容
 如图,已知椭圆C:
如图,已知椭圆C: 的离心率为
的离心率为 ,以椭圆C的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0),设圆T与椭圆C交于点M与点N.
,以椭圆C的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0),设圆T与椭圆C交于点M与点N.(1)求椭圆C的方程;
(2)求
 的最小值,并求此时圆T的方程;
的最小值,并求此时圆T的方程;(3)设点P是椭圆C上异于M,N的任意一点,且直线MP,NP分别与x轴交于点R,S,O为坐标原点,求证:|OR|•|OS|为定值.
【答案】分析:(1)依题意,得a=2, ,由此能求出椭圆C的方程.
,由此能求出椭圆C的方程.
(2)法一:点M与点N关于x轴对称,设M(x1,y1),N(x1,-y1),设y1>0.由于点M在椭圆C上,故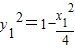 .由T(-2,0),知
.由T(-2,0),知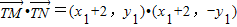 =
=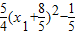 ,由此能求出圆T的方程.
,由此能求出圆T的方程.
法二:点M与点N关于x轴对称,故设M(2cosθ,sinθ),N(2cosθ,-sinθ),设sinθ>0,由T(-2,0),得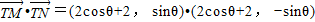 =
=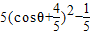 ,由此能求出圆T的方程.
,由此能求出圆T的方程.
(3)法一:设P(x,y),则直线MP的方程为: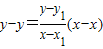 ,令y=0,得
,令y=0,得 ,同理:
,同理: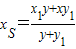 ,…(10分)故
,…(10分)故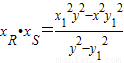 ,由此能够证明|OR|•|OS|=|xR|•|xS|=|xR•xS|=4为定值.
,由此能够证明|OR|•|OS|=|xR|•|xS|=|xR•xS|=4为定值.
法二:设M(2cosθ,sinθ),N(2cosθ,-sinθ),设sinθ>0,P(2cosα,sinα),其中sinα≠±sinθ.则直线MP的方程为: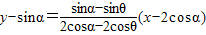 ,由此能够证明|OR|•|OS|=|xR|•|xS|=|xR•xS|=4为定值.
,由此能够证明|OR|•|OS|=|xR|•|xS|=|xR•xS|=4为定值.
解答:解:(1)依题意,得a=2, ,
,
∴c=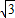 ,b=
,b=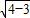 =1,
=1,
故椭圆C的方程为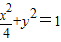 .…(3分)
.…(3分)
(2)方法一:点M与点N关于x轴对称,
设M(x1,y1),N(x1,-y1),不妨设y1>0.
由于点M在椭圆C上,所以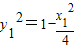 . (*) …(4分)
. (*) …(4分)
由已知T(-2,0),则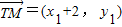 ,
,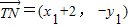 ,
,
∴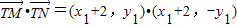
=(x1+2)2-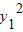
=
=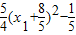 .…(6分)
.…(6分)
由于-2<x1<2,
故当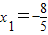 时,
时,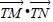 取得最小值为
取得最小值为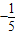 .
.
由(*)式,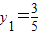 ,故
,故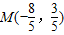 ,
,
又点M在圆T上,代入圆的方程得到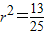 .
.
故圆T的方程为: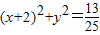 .…(8分)
.…(8分)
方法二:点M与点N关于x轴对称,
故设M(2cosθ,sinθ),N(2cosθ,-sinθ),
不妨设sinθ>0,由已知T(-2,0),
则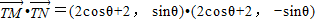
=(2cosθ+2)2-sin2θ
=5cos2θ+8cosθ+3
=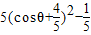 .…(6分)
.…(6分)
故当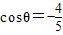 时,
时, 取得最小值为
取得最小值为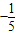 ,
,
此时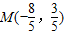 ,
,
又点M在圆T上,代入圆的方程得到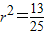 .
.
故圆T的方程为: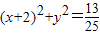 . …(8分)
. …(8分)
(3)方法一:设P(x,y),
则直线MP的方程为: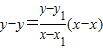 ,
,
令y=0,得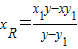 ,
,
同理: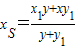 ,…(10分)
,…(10分)
故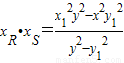 (**) …(11分)
(**) …(11分)
又点M与点P在椭圆上,
故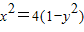 ,
,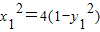 ,…(12分)
,…(12分)
代入(**)式,
得: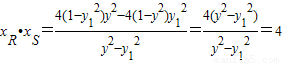 .
.
所以|OR|•|OS|=|xR|•|xS|=|xR•xS|=4为定值. …(14分)
方法二:设M(2cosθ,sinθ),N(2cosθ,-sinθ),
不妨设sinθ>0,P(2cosα,sinα),其中sinα≠±sinθ.
则直线MP的方程为: ,
,
令y=0,得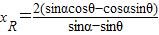 ,
,
同理: ,…(12分)
,…(12分)
故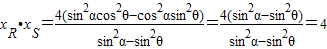 .
.
所以|OR|•|OS|=|xR|•|xS|=|xR•xS|=4为定值.…(14分)
点评:本题考查椭圆的方程和几何性质、圆的方程等基础知识,考查运算求解能力、推理论证能力,考查函数与方程思想、数形结合思想.
 ,由此能求出椭圆C的方程.
,由此能求出椭圆C的方程.(2)法一:点M与点N关于x轴对称,设M(x1,y1),N(x1,-y1),设y1>0.由于点M在椭圆C上,故
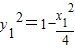 .由T(-2,0),知
.由T(-2,0),知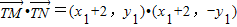 =
=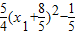 ,由此能求出圆T的方程.
,由此能求出圆T的方程.法二:点M与点N关于x轴对称,故设M(2cosθ,sinθ),N(2cosθ,-sinθ),设sinθ>0,由T(-2,0),得
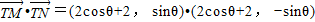 =
=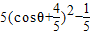 ,由此能求出圆T的方程.
,由此能求出圆T的方程.(3)法一:设P(x,y),则直线MP的方程为:
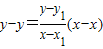 ,令y=0,得
,令y=0,得 ,同理:
,同理: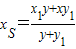 ,…(10分)故
,…(10分)故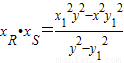 ,由此能够证明|OR|•|OS|=|xR|•|xS|=|xR•xS|=4为定值.
,由此能够证明|OR|•|OS|=|xR|•|xS|=|xR•xS|=4为定值. 法二:设M(2cosθ,sinθ),N(2cosθ,-sinθ),设sinθ>0,P(2cosα,sinα),其中sinα≠±sinθ.则直线MP的方程为:
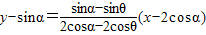 ,由此能够证明|OR|•|OS|=|xR|•|xS|=|xR•xS|=4为定值.
,由此能够证明|OR|•|OS|=|xR|•|xS|=|xR•xS|=4为定值.解答:解:(1)依题意,得a=2,
 ,
,∴c=
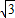 ,b=
,b=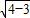 =1,
=1,故椭圆C的方程为
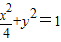 .…(3分)
.…(3分)(2)方法一:点M与点N关于x轴对称,
设M(x1,y1),N(x1,-y1),不妨设y1>0.
由于点M在椭圆C上,所以
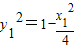 . (*) …(4分)
. (*) …(4分)由已知T(-2,0),则
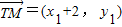 ,
,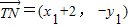 ,
,∴
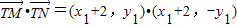
=(x1+2)2-
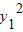
=

=
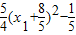 .…(6分)
.…(6分)由于-2<x1<2,
故当
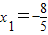 时,
时,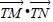 取得最小值为
取得最小值为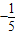 .
.由(*)式,
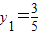 ,故
,故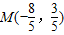 ,
,又点M在圆T上,代入圆的方程得到
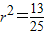 .
.故圆T的方程为:
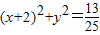 .…(8分)
.…(8分)方法二:点M与点N关于x轴对称,
故设M(2cosθ,sinθ),N(2cosθ,-sinθ),
不妨设sinθ>0,由已知T(-2,0),
则
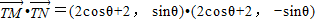
=(2cosθ+2)2-sin2θ
=5cos2θ+8cosθ+3
=
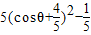 .…(6分)
.…(6分)故当
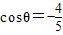 时,
时, 取得最小值为
取得最小值为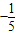 ,
,此时
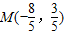 ,
,又点M在圆T上,代入圆的方程得到
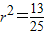 .
.故圆T的方程为:
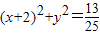 . …(8分)
. …(8分)(3)方法一:设P(x,y),
则直线MP的方程为:
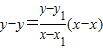 ,
,令y=0,得
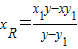 ,
,同理:
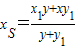 ,…(10分)
,…(10分)故
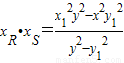 (**) …(11分)
(**) …(11分)又点M与点P在椭圆上,
故
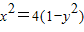 ,
,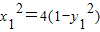 ,…(12分)
,…(12分)代入(**)式,
得:
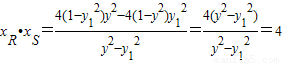 .
.所以|OR|•|OS|=|xR|•|xS|=|xR•xS|=4为定值. …(14分)
方法二:设M(2cosθ,sinθ),N(2cosθ,-sinθ),
不妨设sinθ>0,P(2cosα,sinα),其中sinα≠±sinθ.
则直线MP的方程为:
 ,
,令y=0,得
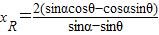 ,
,同理:
 ,…(12分)
,…(12分)故
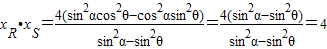 .
.所以|OR|•|OS|=|xR|•|xS|=|xR•xS|=4为定值.…(14分)
点评:本题考查椭圆的方程和几何性质、圆的方程等基础知识,考查运算求解能力、推理论证能力,考查函数与方程思想、数形结合思想.

练习册系列答案
相关题目
 (2013•临沂二模)
(2013•临沂二模) 的左、右焦点分别为
的左、右焦点分别为 ,离心率为
,离心率为 ,点A是椭圆上任一点,
,点A是椭圆上任一点, 的周长为
的周长为 .
. 任作一动直线l交椭圆C于
任作一动直线l交椭圆C于 两点,记
两点,记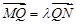 ,若在线段
,若在线段 上取一点R,使得
上取一点R,使得 ,则当直线l转动时,点R在某一定直线上运动,求该定直线的方程.
,则当直线l转动时,点R在某一定直线上运动,求该定直线的方程.
 的上、下顶点分别为A、B,点P在椭圆C上且异于点A、B,直线AP、PB与直线l:y=-2分别交于点M、N.
的上、下顶点分别为A、B,点P在椭圆C上且异于点A、B,直线AP、PB与直线l:y=-2分别交于点M、N.
 的长轴AB长为4,离心率
的长轴AB长为4,离心率 ,O为坐标原点,过B的直线l与x轴垂直.P是椭圆上异于A、B的任意一点,PH⊥x轴,H为垂足,延长HP到点Q使得HP=PQ,连接AQ延长交直线l于点M,N为MB的中点.
,O为坐标原点,过B的直线l与x轴垂直.P是椭圆上异于A、B的任意一点,PH⊥x轴,H为垂足,延长HP到点Q使得HP=PQ,连接AQ延长交直线l于点M,N为MB的中点.