题目内容
(本小题满分12分)在△ABC中,a、b、c分别是角A、B、C的对边,且 ,
,
(1)求∠A的度数;
(2)若a= ,b+c=3,求b和c的值.
,b+c=3,求b和c的值.
 ,
,(1)求∠A的度数;
(2)若a=
 ,b+c=3,求b和c的值.
,b+c=3,求b和c的值.(1)=60°;(2) 或
或
 或
或
解:(1)由4sin2 -cos2A=
-cos2A= 及A+B+C=180°,
及A+B+C=180°,
得2[1-cos(B+C)]-2cos2A+1= ,
,
4(1+cosA)-4cos2A=5.
∴4cos2A-4cosA+1=0,∴cosA= .
.
∵0°<A<180°,∴A=60°. 6分
(2)由余弦定理得:cosA= .
.
∵cosA= ,∴
,∴ =
=  , ∴(b+c)2-a2=3bc.
, ∴(b+c)2-a2=3bc.
将a= ,b+c=3代入上式得bc=2.
,b+c=3代入上式得bc=2.
由 得
得 或
或 12分
12分
 -cos2A=
-cos2A= 及A+B+C=180°,
及A+B+C=180°,得2[1-cos(B+C)]-2cos2A+1=
 ,
,4(1+cosA)-4cos2A=5.
∴4cos2A-4cosA+1=0,∴cosA=
 .
.∵0°<A<180°,∴A=60°. 6分
(2)由余弦定理得:cosA=
 .
.∵cosA=
 ,∴
,∴ =
=  , ∴(b+c)2-a2=3bc.
, ∴(b+c)2-a2=3bc.将a=
 ,b+c=3代入上式得bc=2.
,b+c=3代入上式得bc=2.由
 得
得 或
或 12分
12分
练习册系列答案
相关题目
 ,b=
,b= ,∠A=30°,则c等于( ).
,∠A=30°,则c等于( ). 或
或 的内角
的内角 的对边分别为
的对边分别为 ,若
,若 ,
, =
= ,
, =
= ,B=60°,那么满足条件的三角形的个数为( )
,B=60°,那么满足条件的三角形的个数为( ) 的对边分别是
的对边分别是 ,已知
,已知 .
. 的值;
的值; ,求边
,求边 的值.
的值.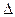 ABC的三边
ABC的三边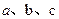 和面积
和面积 满足:
满足: 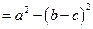 ,且
,且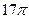 ,则面积
,则面积 中,若
中,若 ,则
,则 _________
_________