题目内容
△ABC中,根据下列条件,确定△ABC有两解的是
| A.a=18,b=20,A=120° | B.a=60,c=48,B=60° | C.a=3,b=6,A=30° | D.a=14,b=16,A=45° |
D
分析:A中,由a=18,b=20,可得B>A>120°,故三角形无解.
B中,由a=60,c=48,B=60°,再由余弦定理可得b值唯一,故三角形有唯一解.
C 中,由正弦定理解得 sinB=1,B=90°,故三角形有唯一解.
D中,由正弦定理可得 sinB=
 >sin45°,故B可能是锐角,也可能是钝角,故三角形有两解.
>sin45°,故B可能是锐角,也可能是钝角,故三角形有两解.解:A中,a=18,b=20,故有 B>A>120°,这与三角形的内角和相矛盾,故三角形无解.
B中,∵a=60,c=48,B=60°,由余弦定理可得 b=
 ,故三角形有唯一解.
,故三角形有唯一解.C 中,a=3,b=6,A=30°,由正弦定理可得
 =
=  ,解得 sinB=1,∴B=90°,故三角形有唯一解.
,解得 sinB=1,∴B=90°,故三角形有唯一解.D中,a=14,b=16,A=45°,由正弦定理可得
 =
= ,∴sinB=
,∴sinB= >sin45°,
>sin45°,故B 可能是锐角,也可能是钝角,故三角形有两解.
故选D.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
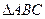 中,角
中,角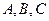 所对的边分别为
所对的边分别为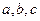 ,满足
,满足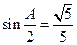 ,且
,且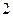 .
.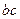 的值
的值 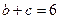 ,求
,求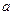 的值.
的值. 则
则 ( )
( )



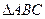 中角
中角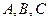 所对的边长分别为
所对的边长分别为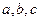 ,且
,且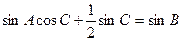 .
.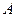 的大小; (Ⅱ)若
的大小; (Ⅱ)若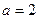 ,求
,求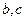 值.
值. ,
, ,b+c=3,求b和c的值.
,b+c=3,求b和c的值. 中。若b=5,
中。若b=5, ,tanA=2,则sinA=____________;a=_______________。
,tanA=2,则sinA=____________;a=_______________。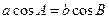 ,则这个三角形的形状是 三角形
,则这个三角形的形状是 三角形 中,角
中,角 所对的边分别为
所对的边分别为 ,若
,若 ,则
,则 ________。
________。