题目内容

证明函数：f（x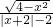）= $数学公式$ 的奇偶性．

证明：∵ $\text{[math]}$ ∴定义域为[-2，0）∪（0，2]．
所以f（x）= $\text{[math]}$ ，所以f（-x）= $\text{[math]}$ ．
所以f（x）为奇函数．
分析：证明函数的奇偶性一般要先看函数的定义域，故本题要先研究出函数的定义域，看其是否关于原点对称，若不对称，可直接下结论，若对称，再利用定义证明
点评：本题考查函数奇偶性的判断，求解本题，关键是根据函数的解析式求出函数的定义域，再对函数的解析式进行化简，熟练掌握函数奇偶性的判断方法也是解决本题的关键条件之一．

练习册系列答案

夺冠金卷系列答案

期末考试金钥匙系列答案

45分钟课时作业与单元测试系列答案

必会必考精讲点练系列答案

步步高名校练考卷系列答案

高中金牌单元测试系列答案

名师一号高中同步学习方略系列答案

华夏1卷通系列答案

课时方案新版新理念导学与测评系列答案

相关题目

19、已知函数y=f（x）（x∈R）满足f（a+x）=f（a-x）（a≠0）
（1）求证：y=f（x）的图象关于直线x=a对称．
（2）又若函数y=f（x）的图象在于直线x=b（b≠a）对称，证明函数y=f（x）是周期函数．

证明函数：f（x）=

的奇偶性．

已知函数f(x)=

(a∈R)，
（1）证明函数y=f（x）的图象关于点（a，-1）成中心对称图形；
（2）当x∈[a+1，a+2]时，求证：f（x）∈[-2，-

]；
（3）我们利用函数y=f（x）构造一个数列{x_n}，方法如下：对于给定的定义域中的x₁，令x₂=f（x₁），x₃=f（x₂），…，x_n=f（x_n-1），…在上述构造数列的过程中，如果xi（i=2，3，4，…）在定义域中，构造数列的过程将继续下去；如果x_i不在定义域中，则构造数列的过程停止．
（i）如果可以用上述方法构造出一个常数列{x_n}，求实数a的取值范围；
（ii）如果取定义域中任一值作为x₁，都可以用上述方法构造出一个无穷数列{x_n}，求实数a的值．

若函数f（x）为奇函数，当x≥0时，f（x）=2x²-4x（如图）．
（Ⅰ）请补全函数f（x）的图象；
（Ⅱ）写出函数f（x）的表达式；
（Ⅲ）用定义证明函数y=f（x）在区间[1，+∞）上单调递增．

已知定义在R上恒不为0的函数y=f（x），当x＞0时，满足f（x）＞1，且对于任意的实数x，y都有f（x+y）=f（x）f（y）．
（1）求f（0）的值；
（2）证明f(-x)=-

；
（3）证明函数y=f（x）是R上的增函数．