题目内容
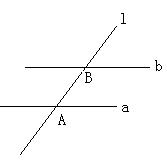
18.(本小题满分13分)如图,平面 ⊥平面
⊥平面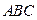 ,
, ,
,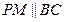 ,
,
直线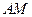 与直线
与直线 所成的角为
所成的角为 ,又
,又 。
。
(1)求证: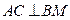 ;
;
(2)求二面角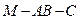 的余弦值
的余弦值
 解:
解: 面
面
 ┅┅┅┅2分
┅┅┅┅2分
如图以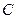 为原点建立空间直角坐标系
为原点建立空间直角坐标系 .
.
设
 则
则 ,
, ,
, .
. 
 ,
,
由直线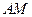 与直线
与直线 所成的角为60°,得
所成的角为60°,得 ,即
,即 ,解得
,解得 .┅┅┅4分
.┅┅┅4分
(1)∴ ,
, ,得
,得 ┅┅┅6分
┅┅┅6分
∴ ,
, ┅┅┅8分
┅┅┅8分
(2)设平面 的一个法向量为
的一个法向量为 ,则
,则
由 ,取
,取 ,得
,得 ┅┅┅┅10分
┅┅┅┅10分
取平面 的一个法向量为
的一个法向量为
则
 ┅┅┅┅12分
┅┅┅┅12分
由图知二面角 的大小的余弦值为
的大小的余弦值为 ┅┅┅┅13分
┅┅┅┅13分
方法二:(1)因为 ┅┅┅3分
┅┅┅3分 ┅┅┅6分
┅┅┅6分
(2)同上
解析

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知 =(2,4,5),
=(2,4,5), =(3,x,y),若
=(3,x,y),若 ∥
∥ ,则( )
,则( )
| A.x=6,y=15 |
B.x=3,y= |
| C.x=3,y=15 |
D.x=6,y= |
 中,
中, ,
,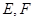 是
是 和
和 的中点.(Ⅰ)求证:
的中点.(Ⅰ)求证: 平面
平面 ;
; ,求
,求
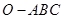 中,
中, 、
、 、
、 两两垂直,且
两两垂直,且 ,
,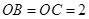 ,点
,点 是棱
是棱 与
与 所成角的余弦值;
所成角的余弦值; 的余弦值.
的余弦值.

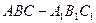 中,底面
中,底面 是边长为2的正三角形,侧棱长为3,且侧棱
是边长为2的正三角形,侧棱长为3,且侧棱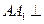 面
面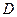 是
是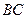 的中点.
的中点.
 ;
; 平面
平面 .
. ,求证:
,求证: .
.
 ,M、N分别为AB、SB的中点。
,M、N分别为AB、SB的中点。
 中,AB=AD=1,AA1=2,M是棱CC1的中点
中,AB=AD=1,AA1=2,M是棱CC1的中点