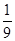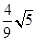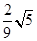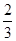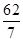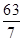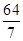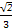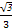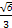题目内容
(14分)(理)在三棱锥S-ABC中,△ABC是边长为4的正三角形,平面SAC
⊥平面ABC,SA=SC=2 ,M、N分别为AB、SB的中点。
,M、N分别为AB、SB的中点。
(Ⅰ)证明:AC⊥SB;
(Ⅱ)求二面角N-CM-B的大小;
(Ⅲ)求点B到平面CMN的距离.
解法一:(Ⅰ)取AC中点D,连结SD、DB.
∵SA=SC,AB=BC,∴AC⊥SD且AC⊥BD,∴AC⊥平面SDB,又SB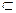 平面SDB,
平面SDB,
∴AC⊥SB.
(Ⅱ)∵AC⊥平面SDB,AC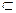 平面ABC,∴平面SDB⊥平面ABC.过N作NE⊥BD于E,NE⊥平面ABC,过E作EF⊥CM于F,连结NF,则NF⊥CM.∴∠NFE为二面角
平面ABC,∴平面SDB⊥平面ABC.过N作NE⊥BD于E,NE⊥平面ABC,过E作EF⊥CM于F,连结NF,则NF⊥CM.∴∠NFE为二面角
N-CM-B的平面角.∵平面SAC⊥平面ABC,SD⊥AC,
∴SD⊥平面ABC.又∵NE⊥平面ABC,∴NE∥SD.
∵SN=NB,∴NE= SD=
SD=
 =
=
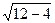 =
= ,
,
且ED=EB.在正△ABC中,由平几知 识可求得EF=
识可求得EF= MB=
MB= ,在Rt△N
,在Rt△N EF中,tan∠
EF中,tan∠
NFE= =2
=2 ,∴二面角N-CM-B的大小是arctan2
,∴二面角N-CM-B的大小是arctan2 .
.
(Ⅲ)在Rt△NEF中,NF= =
= ,∴S△CMN=
,∴S△CMN= CM·NF=
CM·NF=
 ,S△
,S△
CMB= BM·CM=2
BM·CM=2 .
.
设点B到平面CMN的距离为h,∵VB-CMN=VN-CMB,NE⊥平面CMB,∴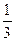 S△CMN·h=
S△CMN·h=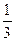 S△CMB·NE,
S△CMB·NE,
∴h= =
= .即点B到平面CMN的距离为
.即点B到平面CMN的距离为 .
.
解法二:(Ⅰ)取AC中点O,连结OS、O B.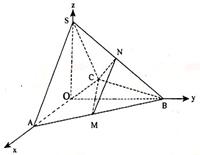
∵SA= SC,AB=BC,∴AC⊥SO且AC⊥BO.
SC,AB=BC,∴AC⊥SO且AC⊥BO.
∵平面SAC⊥平面ABC,平面SAC ∩平面ABC=AC∴SO⊥面ABC,∴SO
∩平面ABC=AC∴SO⊥面ABC,∴SO ⊥BO.
⊥BO.
如图所示建立空间直角坐标系O-xyz.则A(2,0,0),B(0,2 ,0),C(-2,0,0),S(0,0,2
,0),C(-2,0,0),S(0,0,2 ),M(1,
),M(1, ,0),N(0,
,0),N(0, ,
, ).∴
).∴ =(-4,0,0),
=(-4,0,0), =(0,2
=(0,2 ,2
,2 ),
),
∵ ·
·
 =(-4,0,0)·(0,2
=(-4,0,0)·(0,2 ,2
,2 )=0,∴AC⊥SB.
)=0,∴AC⊥SB.
(Ⅱ)由(Ⅰ)得 =(3,
=(3, ,0),
,0),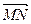 =(-1,0,
=(-1,0, ).
).
设 =(x,y,z)为平面CMN的一个法向量,则
=(x,y,z)为平面CMN的一个法向量,则
取z=1,则x= ,y=-
,y=- ,∴
,∴ =(
=( ,-
,- ,1),
,1),
又 =(0,0,2
=(0,0,2 )为平面ABC的一个法向量,
)为平面ABC的一个法向量,
∴cos( ,
, )=
)=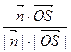 =
=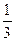 .
.
∴二面角N-CM-B的大小为arccos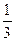 .
.
(Ⅲ)由(Ⅰ)(Ⅱ)得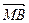 =(-1,
=(-1, ,0),
,0),
解析

 备战中考寒假系列答案
备战中考寒假系列答案已知向量 ,
, ,则以
,则以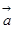 ,
, 为邻边的平行四边形的面积为( )
为邻边的平行四边形的面积为( )
A. | B.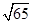 | C.4 | D.8 |

 ⊥平面
⊥平面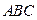 ,
, ,
,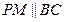 ,
,
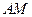 与直线
与直线 所成的角为
所成的角为 ,又
,又 。
。 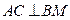 ;
;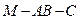 的余弦值
的余弦值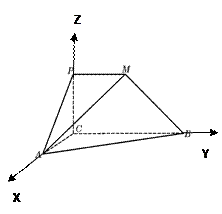
 使得BE⊥CE,求线段AD的取值范围,并求当线段PD上有且只
使得BE⊥CE,求线段AD的取值范围,并求当线段PD上有且只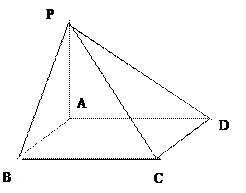

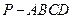 中,侧棱
中,侧棱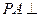 平面
平面 ,底面
,底面 ,
,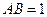 ,
, ,
, 分别是
分别是 的中点.
的中点. 平面
平面
 与底面
与底面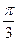 时,求二面角
时,求二面角 的大小.
的大小.
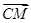 ,
,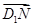 〉的值为( )
〉的值为( )