题目内容
已知A(0,k),B(1,2),C(3,4)三点共线,则k=
1
1
.分析:根据A,B,C三点共线可得KAB=KBC然后利用两点间的斜率公式代入求解即可.
解答:解:∵A(0,k),B(1,2),C(3,4)三点共线
∴KAB=KBC
∴
=
∴k=1
故答案为1
∴KAB=KBC
∴
| 2-k |
| 1-0 |
| 4-2 |
| 3-1 |
∴k=1
故答案为1
点评:本题主要考查了点共线的问题.解题的关键是要将点共线问题转化为直线的斜率相等问题然后再利用两点间斜率公式KAB=
代入求解!
| y2-y1 |
| x2-x1 |

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
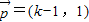 ,则“k=2”是“
,则“k=2”是“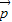 ∥
∥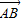 ”的( )
”的( )