题目内容
【题目】已知等比数列{an}的前n项和为Sn ， 且 
（a∈N+）．
（1）求a的值及数列{an}的通项公式；
（2）设 
，求{bn}的前n项和Tn ．
【答案】解：（1）∵等比数列{an}满足 
（a∈N+），
∴当n=1时，6a1=9+a；
当n≥2时， 
．
∴ 
，
∵n=1时也成立，∴1×6=9+a，解得a=﹣3，
∴ ；
（2） 
= 
= 
．
当n为奇数时， 
；
当n为偶数时，Tn= 
．
综上， 
．
【解析】（1）先求得n=1的情况，再根据关系式，求得n≥2时{an}的通项公式，最后验证n=1的情况是否满足通项公式；（2）将（1）中求得的{an}的通项公式代入{bn}中，从而求得{bn}的通项公式，求前n项和时分n为奇数与n为偶数的情况进行计算，算的后借助-1的指数幂进行统一表示.
【考点精析】掌握数列的前n项和和数列的通项公式是解答本题的根本，需要知道数列{an}的前n项和sn与通项an的关系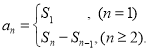
；如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式．
练习册系列答案
相关题目
