题目内容
如图,在棱长均为1的三棱锥S-ABC中,E为棱SA的中点,F为△ABC的中心,则直线EF与平面ABC所成角的正切值是( )
A.

B.1
C.

D.

【答案】分析:连接SF,AF,则SF⊥平面ABC,取AF的中点O,则EO⊥平面ABC,可得∠EFO是直线EF与平面ABC所成角,求出EO,OF,即可求直线EF与平面ABC所成角的正切值.
解答: 解:连接SF,AF,则
解:连接SF,AF,则
∵F为△ABC的中心,∴SF⊥平面ABC
取AF的中点O,则∵E为棱SA的中点,
∴EO∥SF
∴EO⊥平面ABC
∴∠EFO是直线EF与平面ABC所成角,
∵棱长为1
∴AF= ,SF=
,SF= =
=
∴OF= ,
,
∴tan∠EFO= =
= =
=
故选C.
点评:本题考查线面角,考查学生的计算能力,正确作出线面角是关键.
解答:
 解:连接SF,AF,则
解:连接SF,AF,则∵F为△ABC的中心,∴SF⊥平面ABC
取AF的中点O,则∵E为棱SA的中点,
∴EO∥SF
∴EO⊥平面ABC
∴∠EFO是直线EF与平面ABC所成角,
∵棱长为1
∴AF=
 ,SF=
,SF= =
=
∴OF=
 ,
,
∴tan∠EFO=
 =
= =
=
故选C.
点评:本题考查线面角,考查学生的计算能力,正确作出线面角是关键.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
 (2010•泰安一模)如图,在棱长均为1的三棱锥S-ABC中,E为棱SA的中点,F为△ABC的中心,则直线EF与平面ABC所成角的正切值是( )
(2010•泰安一模)如图,在棱长均为1的三棱锥S-ABC中,E为棱SA的中点,F为△ABC的中心,则直线EF与平面ABC所成角的正切值是( )




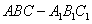 中,
中,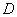 、
、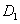 分别是
分别是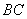 、
、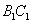 的中点。
的中点。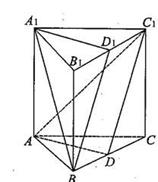 求证:平面
求证:平面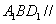 平面
平面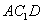 ;
;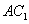 与
与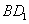 所成角的余弦值
所成角的余弦值