题目内容
在平面直角坐标系xOy中,双曲线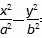 =1(a>0,b>0)的两条渐近线与抛物线y2=4x的准线相交于A,B两点.若△AOB的面积为2,则双曲线的离心率为 .
=1(a>0,b>0)的两条渐近线与抛物线y2=4x的准线相交于A,B两点.若△AOB的面积为2,则双曲线的离心率为 .
练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案
相关题目
题目内容
在平面直角坐标系xOy中,双曲线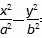 =1(a>0,b>0)的两条渐近线与抛物线y2=4x的准线相交于A,B两点.若△AOB的面积为2,则双曲线的离心率为 .
=1(a>0,b>0)的两条渐近线与抛物线y2=4x的准线相交于A,B两点.若△AOB的面积为2,则双曲线的离心率为 .
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案