题目内容

已知椭圆C：
x2
4
+
y2
3
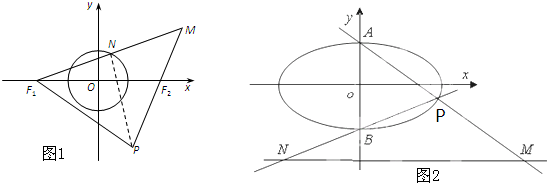
=1的左、右焦点分别为F1，F2，椭圆C上点A满足AF2⊥F1F2．若点P是椭圆C上的动点，则
F1P
?
F2A
的最大值为（　　）
A、
3
2
B、
3
3
2
C、
9
4
D、
15
4
分析：由已知可得点A，F1，F2的坐标，再利用数量积运算法则和点P的纵坐标的取值范围即可得出最大值．
解答：解：如图所示，由椭圆C：
x2
4
+
y2
3
=1可得：a2=4，b2=3，c=
a2-b2
=1．∴F1（-1，0），F2（1，0）．
∵AF2⊥F1F2，∴A(1，
3
2
)．
设P（x，y），则
x2
4
+
y2
3
=1．又-
3
≤y≤
3
，
∴
F1P
•
F2A
=(x+1，y)•(0，
3
2
)=
3
2
y≤
3
3
2
．
∴
F1P
•
F2A
的最大值为
3
3
2
．
故选：B．
点评：本题考查了椭圆的标准方程及其性质、数量积运算等基础知识与基本技能方法，属于基础题．
练习册系列答案
相关题目
精英家教网圆锥曲线上任意两点连成的线段称为弦．若圆锥曲线上的一条弦垂直于其对称轴，我们将该弦称之为曲线的垂轴弦．已知椭圆C：
x2
4
+y2=1．
（1）过椭圆C的右焦点作一条垂直于x轴的垂轴弦MN，求MN的长度；
（2）若点P是椭圆C上不与顶点重合的任意一点，MN是椭圆C的短轴，直线MP、NP分别交x轴于点E（xE，0）和点F（xF，0）（如图），求xE?xF的值；
（3）在（2）的基础上，把上述椭圆C一般化为
x2
a2
+
y2
b2
=1(a＞b＞0)，MN是任意一条垂直于x轴的垂轴弦，其它条件不变，试探究xE?xF是否为定值？（不需要证明）；请你给出双曲线
x2
a2
-
y2
b2
=1(a＞0，b＞0)中相类似的结论，并证明你的结论．
已知椭圆C：
x24
+y2=1，直线l与椭圆C相交于A、B两点，若以AB为直径的圆经过坐标原点．
（1）试探究：点O到直线AB的距离是否为定值，若是，求出该定值；若不是，请说明理由；
（2）求△AOB面积S的最小值．
（2013•房山区一模）已知椭圆C：
x2
4
+
y2
3
=1和点P（4，0），垂直于x轴的直线与椭圆C交于A，B两点，连结PB交椭圆C于另一点E．
（Ⅰ）求椭圆C的焦点坐标和离心率；
（Ⅱ）证明直线AE与x轴相交于定点．
（2012•安徽模拟）已知椭圆C：
x2
4
+y2=1，直线l与椭圆C相交于A、B两点，
OA
•
OB
=0（其中O为坐标原点）．
（1）试探究：点O到直线AB的距离是否为定值，若是，求出该定值，若不是，请说明理由；
（2）求|OA|•|OB|的最小值．
（1）如图1，已知定点F1（-2，0）、F2（2，0），动点N满足|
ON
|=1（O为坐标原点），
F1M
=2
NM
，
MP
=λ
MF2
（λ∈R），
F1M
•
PN
=0，求点P的轨迹方程．
精英家教网
（2）如图2，已知椭圆C：
x2
4
+y2=1的上、下顶点分别为A、B，点P在椭圆上，且异于点A、B，直线AP、BP与直线l：y=-2分别交于点M、N，
（ⅰ）设直线AP、BP的斜率分别为k1、k2，求证：k1•k2为定值；
（ⅱ）当点P运动时，以MN为直径的圆是否经过定点？请证明你的结论．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网