题目内容
(2012•安徽模拟)已知椭圆C:
+y2=1,直线l与椭圆C相交于A、B两点,
•
=0(其中O为坐标原点).
(1)试探究:点O到直线AB的距离是否为定值,若是,求出该定值,若不是,请说明理由;
(2)求|OA|•|OB|的最小值.
| x2 |
| 4 |
| OA |
| OB |
(1)试探究:点O到直线AB的距离是否为定值,若是,求出该定值,若不是,请说明理由;
(2)求|OA|•|OB|的最小值.
分析:(Ⅰ)点O到直线AB的距离是定值.设A(x1,x2),B(x2,y2),当直线AB的斜率不存在时,则由椭圆的对称性可知,x1=x2,y1=-y2,此时点O到直线AB的距离d=|x1|=
;当直线AB的斜率存在时,设直线AB的方程为y=kx+m,与椭圆C:
+y2 =1联立,得:(1+4k2)x2+8kmx+4m2-4=0,由根与系数的关系得到O到直线AB的距离d=
=
.由此能求出点O到直线AB的距离为定值
.
(Ⅱ)(法一:参数法)设A(x1,y1),B(x2,y2),设直线OA的斜率为k(k≠0),则OA的方程为y=kx,OB的方程为y=-
x,解方程组
,得
,同理可求得
,由此能推导出|OA|•|OB|的最小值.
法二:(均值不等式法)由(Ⅰ)可知,O到直线AB的距离d=
=
.在Rt△OAB中,d=
,故有
=
,由此能求出|OA|•|OB|的最小值.
法三:(三角函数法)由(Ⅰ)知,在Rt△OAB中,点O到直线AB的距离|OH|=
.设∠OAH=θ,则∠BOH=θ,故|OA|=
,|OB|=
.所以,|OA|×|OB|=
=
,由此能求出|OA|•|OB|的最小值.
2
| ||
| 5 |
| x2 |
| 4 |
| |m| | ||
|
2
| ||
| 5 |
2
| ||
| 5 |
(Ⅱ)(法一:参数法)设A(x1,y1),B(x2,y2),设直线OA的斜率为k(k≠0),则OA的方程为y=kx,OB的方程为y=-
| 1 |
| k |
|
|
|
法二:(均值不等式法)由(Ⅰ)可知,O到直线AB的距离d=
| |m| | ||
|
2
| ||
| 5 |
| |OA|×|OB| | ||
|
| |OA|×|OB| | ||
|
2
| ||
| 5 |
法三:(三角函数法)由(Ⅰ)知,在Rt△OAB中,点O到直线AB的距离|OH|=
2
| ||
| 5 |
| |OH| |
| sinθ |
| |OH| |
| cosθ |
| |OH|2 |
| sinθcosθ |
| ||
| sin2θ |
解答:解:(Ⅰ)点O到直线AB的距离是定值.
设A(x1,x2),B(x2,y2),
①当直线AB的斜率不存在时,则由椭圆的对称性可知,x1=x2,y1=-y2,
∵
•
=0,即x1x2+y1y2=0,也就是x12-y12=0,代入椭圆方程解得:|x1| =|y1| =
.
此时点O到直线AB的距离d=|x1|=
.…(2分)
②当直线AB的斜率存在时,设直线AB的方程为y=kx+m,
与椭圆C:
+y2 =1联立,
消去y得:(1+4k2)x2+8kmx+4m2-4=0,
∵x1+x2=-
,x1x2=
,…(3分)
因为OA⊥OB,所以x1x2+y1y2=0,
所以(1+k2)x1x2+km(x1+x2)+m2=0,…(4分)
代入得:(1+k2)
-
+m2=0,
整理得5m2=4(k2+1),…(5分)
O到直线AB的距离d=
=
.
综上所述,点O到直线AB的距离为定值
.…(6分)
(Ⅱ)(法一:参数法)设A(x1,y1),B(x2,y2),设直线OA的斜率为k(k≠0),则OA的方程为y=kx,OB的方程为y=-
x,
解方程组
,得
,
同理可求得
,
故|OA|•|OB|=
|x1|
|x2|
=4
.…(9分)
令1+k2=t(t>1),则|OA|•|OB|=4
=4
,
令g(t)=-
+
+4=-9(
-
)2+
(t>1),所以4<g(t)≤
,即
≤|OA|•|OB|<2.…(11分)
当k=0时,可求得|OA|•|OB|=2,故
≤|OA|•|OB|≤2,故|OA|•|OB|的最小值为
,最大值为2.…(13分)
法二:(均值不等式法)由(Ⅰ)可知,O到直线AB的距离d=
=
.
在Rt△OAB中,d=
,故有
=
,
即(|OA|×|OB|)2=
(|OA|+|OB| 2),…(9分)
而|OA|2+|OB|2≥2|OA|×|OB,(当且仅当|OA|=|OB|时取等号)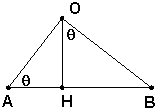
代入上式可得:(|OA|+|OB|)2=
(|OA|2+|OB|2)≥
|OA|×|OB|,
即|OA|×|OB|≥
,(当且仅当|OA|=|OB|时取等号).…(11分)
故|OA|•|OB|的最小值为
.…(13分)
法三:(三角函数法)由(Ⅰ)可知,如图,在Rt△OAB中,点O到直线AB的距离|OH|=
.
设∠OAH=θ,则∠BOH=θ,故|OA|=
,|OB|=
.…(9分)
所以,|OA|×|OB|=
=
,…(11分)
显然,当2θ=
,即θ=
时,|OA|•|OB|取得最小值,最小值为
.…(13分)
设A(x1,x2),B(x2,y2),
①当直线AB的斜率不存在时,则由椭圆的对称性可知,x1=x2,y1=-y2,
∵
| OA |
| OB |
2
| ||
| 5 |
此时点O到直线AB的距离d=|x1|=
2
| ||
| 5 |
②当直线AB的斜率存在时,设直线AB的方程为y=kx+m,
与椭圆C:
| x2 |
| 4 |
消去y得:(1+4k2)x2+8kmx+4m2-4=0,
∵x1+x2=-
| 8km |
| 1+4k2 |
| 4m2-4 |
| 1+4k2 |
因为OA⊥OB,所以x1x2+y1y2=0,
所以(1+k2)x1x2+km(x1+x2)+m2=0,…(4分)
代入得:(1+k2)
| 4m2-4 |
| 1+4k2 |
| 8k2m2 |
| 1+4k2 |
整理得5m2=4(k2+1),…(5分)
O到直线AB的距离d=
| |m| | ||
|
2
| ||
| 5 |
综上所述,点O到直线AB的距离为定值
2
| ||
| 5 |
(Ⅱ)(法一:参数法)设A(x1,y1),B(x2,y2),设直线OA的斜率为k(k≠0),则OA的方程为y=kx,OB的方程为y=-
| 1 |
| k |
解方程组
|
|
同理可求得
|
故|OA|•|OB|=
| 1+k2 |
1+
|
=4
|
令1+k2=t(t>1),则|OA|•|OB|=4
|
|
令g(t)=-
| 9 |
| t2 |
| 9 |
| t |
| 1 |
| t |
| 1 |
| 2 |
| 25 |
| 4 |
| 25 |
| 4 |
| 8 |
| 5 |
当k=0时,可求得|OA|•|OB|=2,故
| 8 |
| 5 |
| 8 |
| 5 |
法二:(均值不等式法)由(Ⅰ)可知,O到直线AB的距离d=
| |m| | ||
|
2
| ||
| 5 |
在Rt△OAB中,d=
| |OA|×|OB| | ||
|
| |OA|×|OB| | ||
|
2
| ||
| 5 |
即(|OA|×|OB|)2=
| 4 |
| 5 |
而|OA|2+|OB|2≥2|OA|×|OB,(当且仅当|OA|=|OB|时取等号)

代入上式可得:(|OA|+|OB|)2=
| 4 |
| 5 |
| 8 |
| 5 |
即|OA|×|OB|≥
| 8 |
| 5 |
故|OA|•|OB|的最小值为
| 8 |
| 5 |
法三:(三角函数法)由(Ⅰ)可知,如图,在Rt△OAB中,点O到直线AB的距离|OH|=
2
| ||
| 5 |
设∠OAH=θ,则∠BOH=θ,故|OA|=
| |OH| |
| sinθ |
| |OH| |
| cosθ |
所以,|OA|×|OB|=
| |OH|2 |
| sinθcosθ |
| ||
| sin2θ |
显然,当2θ=
| π |
| 2 |
| π |
| 4 |
| 8 |
| 5 |
点评:本题探究点到直线的距离是否为定值,求线段乘积的最小值.考查运算求解能力,推理论证能力;考查化归与转化思想.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答.

练习册系列答案
相关题目