题目内容
15.函数y=cosx-cos2x,x∈[-$\frac{π}{2}$,$\frac{π}{2}$]的图象大致为( )| A. | 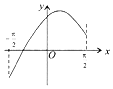 | B. | 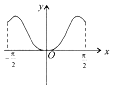 | C. | 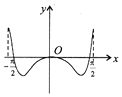 | D. | 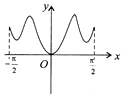 |
分析 判断函数的对称性,极值点的个数,计算函数的最值,从而得出答案.
解答 解:显然=cosx-cos2x是偶函数,图象关于y轴对称,排除A;
y=cosx-(2cos2x-1)=-2cos2x+cosx+1=-2(cosx-$\frac{1}{4}$)2+$\frac{9}{8}$,
∵x∈[-$\frac{π}{2}$,$\frac{π}{2}$],∴0≤cosx≤1,
∴当cosx=1,y取得最小值0,排除C;
y′=-sinx+2sin2x=4sinxcosx-sinx=sinx(4cosx-1),
令y′=0得sinx=0或cosx=$\frac{1}{4}$,而cosx=$\frac{1}{4}$在(-$\frac{π}{2}$,$\frac{π}{2}$)上有两解,
sinx=0在(-$\frac{π}{2}$,$\frac{π}{2}$)上有一解,
∴y=cosx-cos2x在[-$\frac{π}{2}$,$\frac{π}{2}$]上有三个极值点,排除D;
故选B.
点评 本题考查了三角函数恒等变换,函数对称性与最值的计算,属于中档题.

练习册系列答案
相关题目
3.设向量$\overrightarrow{a}$=(2,1),$\overrightarrow{b}$=(0,-2).则与$\overrightarrow{a}$+2$\overrightarrow{b}$垂直的向量可以是( )
| A. | (3,2) | B. | (3,-2) | C. | (4,6) | D. | (4,-6) |
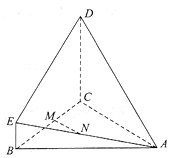 如图,多面体ABCDE中,AB=AC,BE∥CD,BE⊥BC,平面BCDE⊥平面ABC,M为BC的中点.
如图,多面体ABCDE中,AB=AC,BE∥CD,BE⊥BC,平面BCDE⊥平面ABC,M为BC的中点.