题目内容
已知直线l过点P(3,2),且与x轴、y轴的正半轴分别交于A,B两点,如右图所示,
求△ABO的面积的最小值及此时直线l的方程.
审题路线 根据截距式设所求直线l的方程⇒把点P代入,找出截距的关系式⇒运用基本不等式求S△ABO⇒运用取等号的条件求出截距⇒得出直线l的方程.
解 设A(a,0),B(0,b),(a>0,b>0),则直线l的方程为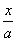 +
+ =1,
=1,
∵l过点P(3,2),∴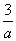 +
+ =1.
=1.
∴1=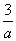 +
+ ≥2
≥2  ,即ab≥24.
,即ab≥24.
∴S△ABO= ab≥12.当且仅当
ab≥12.当且仅当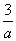 =
= ,即a=6,b=4.
,即a=6,b=4.
△ABO的面积最小,最小值为12.
此时直线l的方程为: +
+ =1.
=1.
即2x+3y-12=0.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某公司生产产品A,产品质量按测试指标分为:指标大于或等于90为一等品,大于或等于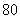 小于
小于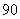 为二等品,小于
为二等品,小于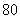 为三等品,生产一件一等品可盈利50元,生产一件二等品可盈利
为三等品,生产一件一等品可盈利50元,生产一件二等品可盈利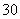 元,生产一件三等品亏损10元.现随机抽查熟练工人甲和新工人乙生产的这种产品各100件进行检测,检测结果统计如下:
元,生产一件三等品亏损10元.现随机抽查熟练工人甲和新工人乙生产的这种产品各100件进行检测,检测结果统计如下:
| 测试指标 |
|
|
|
|
|
|
| 甲 | 3 | 7 | 20 | 40 | 20 | 10 |
| 乙 | 5 | 15 | 35 | 35 | 7 | 3 |
现将根据上表统计得到甲、乙两人生产产品A为一等品、二等品、三等品的频率分别估计为他们生产产品A为一等品、二等品、三等品的概率.
(1)计算新工人乙生产三件产品A,给工厂带来盈利大于或等于100元的概率;
(2)记甲乙分别生产一件产品A给工厂带来的盈利和记为X,求随机变量X的概率分布和数学期望.






 在点(1,1)处的切线与
在点(1,1)处的切线与 轴的交点的横坐标为
轴的交点的横坐标为 ,
, 的值为
的值为 
 x-y+a=0(a为常数)的倾斜角为( ).
x-y+a=0(a为常数)的倾斜角为( ).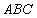 的中线
的中线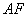 与中位线
与中位线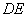 相交于
相交于 ,已知
,已知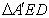 是△
是△ 绕
绕 A.动点
A.动点 在平面
在平面 ⊥平面
⊥平面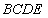
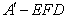 的体积有最大值
的体积有最大值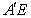 与
与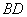 不可能垂直
不可能垂直