题目内容
已知函数 ,求导函数f'(x),并确定f(x)的单调区间.
,求导函数f'(x),并确定f(x)的单调区间.
【答案】分析:根据函数的求导法则进行求导,然后由导数大于0时原函数单调递增,导数小于0时原函数单调递减可得答案.
解答:解: =
= =
= .
.
令f'(x)=0,得x=b-1.
当b-1<1,即b<2时,f'(x)的变化情况如下表:

当b-1>1,即b>2时,f'(x)的变化情况如下表:

所以,当b<2时,函数f(x)在(-∞,b-1)上单调递减,在(b-1,1)上单调递增,
在(1,+∞)上单调递减.
当b>2时,函数f(x)在(-∞,1)上单调递减,在(1,b-1)上单调递增,在(b-1,+∞)上单调递减.
当b-1=1,即b=2时, ,所以函数f(x)在(-∞,1)上单调递减,在(1,+∞)上单调递减.
,所以函数f(x)在(-∞,1)上单调递减,在(1,+∞)上单调递减.
点评:本题主要考查函数的求导方法和导数的应用.导数题一般不会太难但公式记忆容易出错,要熟练掌握简单函数的求导法则.
解答:解:
 =
= =
= .
.令f'(x)=0,得x=b-1.
当b-1<1,即b<2时,f'(x)的变化情况如下表:

当b-1>1,即b>2时,f'(x)的变化情况如下表:

所以,当b<2时,函数f(x)在(-∞,b-1)上单调递减,在(b-1,1)上单调递增,
在(1,+∞)上单调递减.
当b>2时,函数f(x)在(-∞,1)上单调递减,在(1,b-1)上单调递增,在(b-1,+∞)上单调递减.
当b-1=1,即b=2时,
 ,所以函数f(x)在(-∞,1)上单调递减,在(1,+∞)上单调递减.
,所以函数f(x)在(-∞,1)上单调递减,在(1,+∞)上单调递减.点评:本题主要考查函数的求导方法和导数的应用.导数题一般不会太难但公式记忆容易出错,要熟练掌握简单函数的求导法则.

练习册系列答案
相关题目
 ,求导函数f′(x),并确定f(x)的单调区间。
,求导函数f′(x),并确定f(x)的单调区间。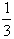 ax3+
ax3+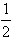 bx2+cx,
bx2+cx,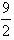 ,x1x3=-12,且a>0,求函数f(x)的单调区间;
,x1x3=-12,且a>0,求函数f(x)的单调区间;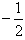 a,3a>2c>2b,试问:导函数f′(x)在区间(0,2)内是否有零点,并说明理由;
a,3a>2c>2b,试问:导函数f′(x)在区间(0,2)内是否有零点,并说明理由;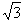 ,求
,求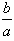 的取值范围。
的取值范围。 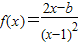 ,求导函数f'(x),并确定f(x)的单调区间.
,求导函数f'(x),并确定f(x)的单调区间. ,求导函数f'(x),并确定f(x)的单调区间.
,求导函数f'(x),并确定f(x)的单调区间.