题目内容
已知函数f(x)=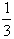 ax3+
ax3+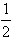 bx2+cx,
bx2+cx,
(Ⅰ)若函数f(x)有三个零点x1,x2,x3,且x1+x2+x3=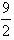 ,x1x3=-12,且a>0,求函数f(x)的单调区间;
,x1x3=-12,且a>0,求函数f(x)的单调区间;
(Ⅱ)若f′(1)=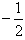 a,3a>2c>2b,试问:导函数f′(x)在区间(0,2)内是否有零点,并说明理由;
a,3a>2c>2b,试问:导函数f′(x)在区间(0,2)内是否有零点,并说明理由;
(Ⅲ)在(Ⅱ)的条件下,若导数f′(x)的两个零点之间的距离不小于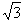 ,求
,求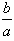 的取值范围。
的取值范围。
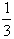 ax3+
ax3+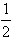 bx2+cx,
bx2+cx,(Ⅰ)若函数f(x)有三个零点x1,x2,x3,且x1+x2+x3=
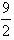 ,x1x3=-12,且a>0,求函数f(x)的单调区间;
,x1x3=-12,且a>0,求函数f(x)的单调区间;(Ⅱ)若f′(1)=
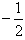 a,3a>2c>2b,试问:导函数f′(x)在区间(0,2)内是否有零点,并说明理由;
a,3a>2c>2b,试问:导函数f′(x)在区间(0,2)内是否有零点,并说明理由;(Ⅲ)在(Ⅱ)的条件下,若导数f′(x)的两个零点之间的距离不小于
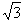 ,求
,求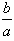 的取值范围。
的取值范围。 解:(Ⅰ) ,
,
∴ ,
,
x1与x3是方程 的两根,
的两根,
 ,
,
由(1)、(2)可知: ,
,
 ,
,
 ;
;
(Ⅱ) ,
,
∴ ,
,
∴ ,
,
 ,
,
 ,
,
①当c>0时,f′(0)>0,f′(1)<0,
∴f′(x)在(0,1)内至少有一个零点;
②当c≤0时,f′(2)>0,f′(1)<0,
∴f′(x)在(1,2)内至少有一个零点;
综上f′(x)在(0,2)内至少有一个零点;
(Ⅲ)设m、n是导函数f′(x)=ax2+bx+c的两个零点,
 ,
,
 ;
;
另一方面:2c=-3a-2b且3a>2c>2b,
∴3a>-3a-2b>2b,
∴ ,
,
∴ ;
;
综上, 。
。
 ,
,∴
 ,
,x1与x3是方程
 的两根,
的两根, ,
,由(1)、(2)可知:
 ,
, ,
, ;
;(Ⅱ)
 ,
,∴
 ,
,∴
 ,
, ,
, ,
,①当c>0时,f′(0)>0,f′(1)<0,
∴f′(x)在(0,1)内至少有一个零点;
②当c≤0时,f′(2)>0,f′(1)<0,
∴f′(x)在(1,2)内至少有一个零点;
综上f′(x)在(0,2)内至少有一个零点;
(Ⅲ)设m、n是导函数f′(x)=ax2+bx+c的两个零点,
 ,
, ;
;另一方面:2c=-3a-2b且3a>2c>2b,
∴3a>-3a-2b>2b,
∴
 ,
,∴
 ;
;综上,
 。
。
练习册系列答案
相关题目