题目内容
已知圆锥曲线E:
+
=4c(c为正常数,过原点O的直线与曲线E交于P、A两点,其中P在第一象限,B是曲线E上不同于P,A的点,直线PB,AB的斜率分别为k1,k2,且k1k2≠0.
(Ⅰ)若P点坐标为(1,
),求圆锥曲线E的标准方程;
(Ⅱ)求k1•k2的值;
(Ⅲ)若PD⊥x轴于点D,D点坐标为(m,0),存在μ∈R使
=μ
,且直线AB与直线l:x=
交于点M,记直线PA、PM的斜率分别为k3,k4,问是否存在常数λ,使k1+k3=λk4,若存在,求出λ的值,若不存在,说明理由.
| (x-c)2+y2 |
| (x+c)2+y2 |
(Ⅰ)若P点坐标为(1,
| 3 |
| 2 |
(Ⅱ)求k1•k2的值;
(Ⅲ)若PD⊥x轴于点D,D点坐标为(m,0),存在μ∈R使
| AD |
| BD |
| 4c2 |
| m |
考点:直线与圆锥曲线的关系,椭圆的简单性质
专题:圆锥曲线中的最值与范围问题
分析:(I)由圆锥曲线E满足:
+
=4c(c为正常数).可得:点E的轨迹是以(±c,0)为焦点,4c为长轴长的椭圆,可得方程为
+
=1.把(1,
)代入解出即可.
(II)设P(x1,y1),B(x2,y2),则A(-x1,-y1).代入椭圆方程相减可得
=-
.利用斜率计算公式可得k1k2=
•
=
即可得出.
(III)设P(x1,y1),则A(-x1,-y1),D(x1,0),直线x=
(m=x1).可得k2=
,k3=
.利用k1k2=-
.可得k1=
.利用A,D,M三点共线可得yM=
(
-x1).得到k4=
=
-
.假设存在常数λ,使k1+k3=λk4,可得
-
=λ(
-
),由于4
=12c2-3
,代入上式可得λ为常数.
| (x-c)2+y2 |
| (x+c)2+y2 |
| x2 |
| 4c2 |
| y2 |
| 3c2 |
| 3 |
| 2 |
(II)设P(x1,y1),B(x2,y2),则A(-x1,-y1).代入椭圆方程相减可得
| ||||
|
| 3 |
| 4 |
| y2-y1 |
| x2-x1 |
| y2+y1 |
| x2+x1 |
| ||||
|
(III)设P(x1,y1),则A(-x1,-y1),D(x1,0),直线x=
| 4c2 |
| m |
| y1 |
| 2x1 |
| y1 |
| x1 |
| 3 |
| 4 |
| -3x1 |
| 2y1 |
| y1 |
| 2x1 |
| 4c2 |
| x1 |
| yM-y1 | ||
|
| y1 |
| 2x1 |
| y1x1 | ||
4c2-
|
| y1 |
| x1 |
| 3x1 |
| 2y1 |
| y1 |
| 2x1 |
| x1y1 | ||
4c2-
|
| y | 2 1 |
| x | 2 1 |
解答:
 解:(I)由圆锥曲线E满足:
解:(I)由圆锥曲线E满足:
+
=4c(c为正常数).
∴点E的轨迹是以(±c,0)为焦点,4c为长轴长的椭圆,
可得方程为
+
=1.
把(1,
)代入可得
+
=1,解得c2=1,
∴椭圆E的标准方程为
+
=1.
(II)设P(x1,y1),B(x2,y2),则A(-x1,-y1).
∴
+
=1,
+
=1,
∴
+
=0,
∴
=-
.
∴k1k2=
•
=
=-
.
(III)设P(x1,y1),则A(-x1,-y1),D(x1,0),直线x=
(m=x1).
k2=
,k3=
.
∵k1k2=-
.
∴k1=
.
∵
=
,
∴yM=
(
-x1).
∴k4=
=
-
.
假设存在常数λ,使k1+k3=λk4,
则
-
=λ(
-
),
化为λ=
×
,
∵4
=12c2-3
,
代入上式可得λ=
×
=2,
∴存在常数λ=2,使k1+k3=λk4成立.
 解:(I)由圆锥曲线E满足:
解:(I)由圆锥曲线E满足:| (x-c)2+y2 |
| (x+c)2+y2 |
∴点E的轨迹是以(±c,0)为焦点,4c为长轴长的椭圆,
可得方程为
| x2 |
| 4c2 |
| y2 |
| 3c2 |
把(1,
| 3 |
| 2 |
| 1 |
| 4c2 |
| 3 |
| 4c2 |
∴椭圆E的标准方程为
| x2 |
| 4 |
| y2 |
| 3 |
(II)设P(x1,y1),B(x2,y2),则A(-x1,-y1).
∴
| ||
| 4c2 |
| ||
| 3c2 |
| ||
| 4c2 |
| ||
| 3c2 |
∴
| ||||
| 3c2 |
| ||||
| 4c2 |
∴
| ||||
|
| 3 |
| 4 |
∴k1k2=
| y2-y1 |
| x2-x1 |
| y2+y1 |
| x2+x1 |
| ||||
|
| 3 |
| 4 |
(III)设P(x1,y1),则A(-x1,-y1),D(x1,0),直线x=
| 4c2 |
| m |
k2=
| y1 |
| 2x1 |
| y1 |
| x1 |
∵k1k2=-
| 3 |
| 4 |
∴k1=
| -3x1 |
| 2y1 |
∵
| yM | ||
|
| y2 |
| 2x1 |
∴yM=
| y1 |
| 2x1 |
| 4c2 |
| x1 |
∴k4=
| yM-y1 | ||
|
| y1 |
| 2x1 |
| y1x1 | ||
4c2-
|
假设存在常数λ,使k1+k3=λk4,
则
| y1 |
| x1 |
| 3x1 |
| 2y1 |
| y1 |
| 2x1 |
| x1y1 | ||
4c2-
|
化为λ=
2
| ||||
|
4c2-
| ||
4c2-3
|
∵4
| y | 2 1 |
| x | 2 1 |
代入上式可得λ=
24c2-18
| ||
12c2-3
|
4c2-
| ||
4c2-3
|
∴存在常数λ=2,使k1+k3=λk4成立.
点评:本题考查了椭圆的定义标准方程及其性质、直线与椭圆相交问题转化为方程联立、斜率计算公式,考查了利用已经证明的结论解决问题的能力,考查了推理能力与计算能力,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列函数中,在(0,+∞)上单调递增,并且是偶函数的是( )
| A、y=x2 |
| B、y=-x3 |
| C、y=-lg|x| |
| D、y=2x |
给出以下四个命题:
①若x,y∈N*,x+y是奇数,则x,y中一个是奇数一个是偶数;
②若-2≤x<3,则(x+2)(x-3)≤0;
③若x=y=0,则x2+y2=0;
④若x2-3x+2=0,则x=1或x=2.
那么( )
①若x,y∈N*,x+y是奇数,则x,y中一个是奇数一个是偶数;
②若-2≤x<3,则(x+2)(x-3)≤0;
③若x=y=0,则x2+y2=0;
④若x2-3x+2=0,则x=1或x=2.
那么( )
| A、①为假命题 |
| B、②的否命题为真 |
| C、③的逆否命题为假 |
| D、④的逆命题为真 |
下列说法错误的是( )
| A、已知命题p为“?x∈[0,+∞),(log32)x≤1”,则¬p是真命题 |
| B、若p∨q为假命题,则p、q均为假命题 |
| C、x>2是x>1充分不必要条件 |
| D、“全等三角形的面积相等”的否命题是假命题 |
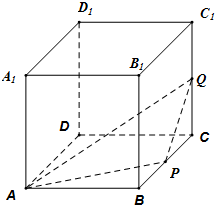 正方体ABCD-A1B1C1D1为棱长为1,动点P,Q分别在棱BC,CC1上,过点A,P,Q的平面截该正方体所得的截面记为S,设BP=x,CQ=y,其中x,y∈[0,1],下列命题正确的是
正方体ABCD-A1B1C1D1为棱长为1,动点P,Q分别在棱BC,CC1上,过点A,P,Q的平面截该正方体所得的截面记为S,设BP=x,CQ=y,其中x,y∈[0,1],下列命题正确的是