已知动圆M恒过定点B2+y2=4外切.求动圆圆心M的轨迹．题目和参考答案——青夏教育精英家教网—

题目内容

已知动圆M恒过定点B（-2，0），且和定圆C：（x-2）²+y²=4外切，求动圆圆心M的轨迹．

考点：轨迹方程

专题：计算题,圆锥曲线的定义、性质与方程

分析：已知条件，知|MC|=r+2，|MB|=r，所以|MC|-|MB|=2，可得点M的轨迹为以C、B为焦点的双曲线的左支，即可得出结论．

解答： 解：圆（x-2）²+y²=4的圆心为C（2，0），半径为2
设动圆圆心为M（x，y），半径为r．
由已知条件，知|MC|=r+2，|MB|=r，
所以|MC|-|MB|=2，
所以点M的轨迹为以C、B为焦点的双曲线的左支．

点评：本题考查轨迹方程，考查双曲线的定义，考查学生分析解决问题的能力，正确运用双曲线的定义是关键．

练习册系列答案

相关题目

各项均为正数的数列{a_n}中，S_n是数列{a_n}的前n项和，且2S_n=a_n²+a_n，
（1）求数列{a_n}的通项公式；
（2）设c为实数，如果对任意的正整数n，不等式

在△ABC中，角A、B、C的对边分别为a、b、c，且a=

，b²+c²-

bc=3．
（Ⅰ）求角A；
（Ⅱ）设cosB=

=4c（c为正常数，过原点O的直线与曲线E交于P、A两点，其中P在第一象限，B是曲线E上不同于P，A的点，直线PB，AB的斜率分别为k₁，k₂，且k₁k₂≠0．
（Ⅰ）若P点坐标为（1，

），求圆锥曲线E的标准方程；
（Ⅱ）求k₁•k₂的值；
（Ⅲ）若PD⊥x轴于点D，D点坐标为（m，0），存在μ∈R使

=μ

，且直线AB与直线l：x=

4c2

交于点M，记直线PA、PM的斜率分别为k₃，k₄，问是否存在常数λ，使k₁+k₃=λk₄，若存在，求出λ的值，若不存在，说明理由．

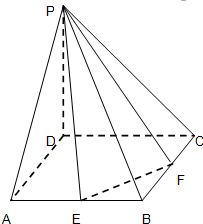已知正方形ABCD，边长为1，过D作PD⊥平面ABCD，且PD=2，E，F分别是AB和BC的中点．
（1）求直线AC到平面PEF的距离；
（2）求直线PB与平面PEF所成角的余弦值．

抛物线y²=2px三点的纵坐标的平方成等差数列，则这三点的横坐标（　　）

已知f（x）=x²-2|x-a|，当a＞O时，若对任意的x∈[O，+∞），不等式f（x-1）≥2f（x）恒成立，求a的值．

试题分类