题目内容
10．设函数$f（x）={log_2}（4x-{x^2}-3）$．（1）求函数f（x）的定义域；
（2）求f（x）的单调区间；
（3）求f（x）的最大值，并求出取得最大值时的x的值．
分析 （1）解4x-x2-3＞0可解函数f（x）的定义域；
（2）由二次函数和复合函数单调性可得；
（3）由（2）可知，当x=2时，函数取最大值，代值计算可得．
解答 解：（1）由4x-x2-3＞0可解得1＜x＜3，
∴函数f（x）的定义域为（1，3）；
（2）二次函数t=4x-x2-3在（1，2）单调递增，在（2，3）单调递减，
由复合函数单调性可得函数f（x）的增区间为（1，2），减区间为（2，3）；
（3）由（2）可知，当x=2时，函数取最大值，
∴函数的最大值为f（x）max=f（2）=0，此时x=2．
点评 本题考查对数函数的图象和性质，涉及复合函数的单调性，属基础题．
练习册系列答案
相关题目
，则下列关系式错误的是（ ）
B．
C．
D．
5．已知函数f（x）=2loga（x-1）（a＞0且a≠1）恒过点（m，n），则在直角坐标系中，函数$g（x）={（\frac{1}{m+n}）^{|{x+1}|}}$的大致图象为（ ）
| A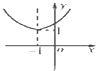． |  | B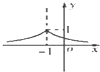． |  | C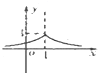． |  | D． |  |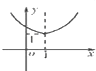
2．设z1、z2∈C，则“z1•z是实数”是“z1、z2互为共轭”的（ ）
| A． | 充分非必要条件 | B． | 必要非充分条件 | ||
| C． | 充要条件 | D． | 既非充分又非必要条件 |
19．下列说法正确的是（ ）
| A． | 终边相同的角相等 | B． | 相等的角终边相同 | ||
| C． | 小于90°的角是锐角 | D． | 第一象限的角是正角 |
18．若2014=αk•5k+αk-1•5k-1+…+a1•51+a0•50，其中ak，ak-1，…，a0∈N，0＜ak＜5，0≤ak-1，ak-2，…，a1，a0＜5．现从a0，a1，…，ak中随机取两个数分别作为点P的横、纵坐标，则点P落在椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=1内的概率是（ ）
| A． | $\frac{11}{25}$ | B． | $\frac{13}{25}$ | C． | $\frac{17}{25}$ | D． | $\frac{11}{16}$ |