题目内容
9.函数f(x)=x2•cosx在$[{-\frac{π}{2},\frac{π}{2}}]$的图象大致是( )| A. | 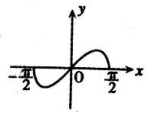 | B. | 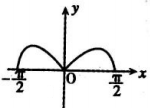 | ||
| C. |  | D. |  |
分析 利用函数的奇偶性,排除选项,利用函数的极值判断即可.
解答 解:函数f(x)=x2•cosx在$[{-\frac{π}{2},\frac{π}{2}}]$,满足f(-x)=f(x),所以函数是偶函数,排除选项A,C;
当x∈(0,$\frac{π}{2}$)时,f′(x)=2xcosx-x2sinx,令2xcosx-x2sinx=0,可得xtanx=2,方程的解x$>\frac{π}{4}$,即函数的极大值点x$>\frac{π}{4}$,排除D,
故选:B.
点评 本题考查函数的奇偶性以及函数的极值的判断,函数的图象的判断,考查计算能力.

练习册系列答案
相关题目
4.已知全集U=Z,A={x∈Z|x2-x-2≥0},B={-1,0,1,2},则(∁UA)∩B=( )
| A. | {-1,2} | B. | {-1,0} | C. | {0,1} | D. | {1,2} |
18.一个三位数,个位、十位、百位上的数字依次为x、y、z,当且仅当y>x,y>z时,称这样的数为“凸数”(如243),现从集合{1,2,3,4}中取出三个不相同的数组成一个三位数,则这个三位数是“凸数”的概率为( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{12}$ |
19.设点F是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的右焦点,点F到渐近线的距离与双曲线的焦距之比为1:4,则双曲线的渐近线方程为( )
| A. | $\sqrt{3}x±y=0$ | B. | $x±\sqrt{3}y=0$ | C. | $\sqrt{15}x±y=0$ | D. | $x±\sqrt{15}y=0$ |