题目内容
已知函数f(x)满足 (其中
(其中 为f(x)在点
为f(x)在点 处的导数,C为常数)。
处的导数,C为常数)。
(1)求 的值;
的值;
(2)求函数f(x)的单调区间;
(3)设函数g(x)=[f(x)-x3]·ex,若函数g(x)在[-3,2]上单调,求实数C的取值范围。
 (其中
(其中 为f(x)在点
为f(x)在点 处的导数,C为常数)。
处的导数,C为常数)。(1)求
 的值;
的值;(2)求函数f(x)的单调区间;
(3)设函数g(x)=[f(x)-x3]·ex,若函数g(x)在[-3,2]上单调,求实数C的取值范围。
解:(1)由f(x)=x3+f' 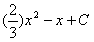
得f'(x)=3x2+2f'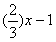
取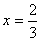 ,得f'
,得f'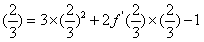
解得f'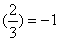 。
。
(2)因为f(x)=x3-x2-x+C
从而f'(x)=3x2-2x-1=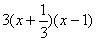 ,列表如下:
,列表如下:

∴f(x)的单调递增区间是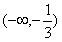 和(1,+∞);
和(1,+∞);
f(x)的单调递减区间是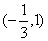 。
。
(3)函数g(x)=[f(x)-x3]·ex=(-x2-x+C)·ex,
有g'(x)=(-2x-1)ex+(-x2-x+C)ex
=(-x2-3x+C-1)ex,
当函数在区间x∈[-3,2]上为单调递增时,
等价于h(x)=-x2-3x+C-1≥0在x∈[-3,2]上恒成立,只要h(2)≥0,解得C≥11,
当函数在区间x∈[-3,2]上为单调递减时,等价于h(x)=-x2-3x+C-1≤0在x∈[-3,2]上恒成立,
即Δ=9+4(C-1)≤0,解得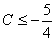
所以C的取值范围是C≥11或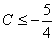 。
。
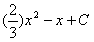
得f'(x)=3x2+2f'
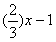
取
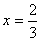 ,得f'
,得f'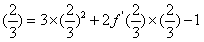
解得f'
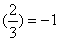 。
。(2)因为f(x)=x3-x2-x+C
从而f'(x)=3x2-2x-1=
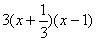 ,列表如下:
,列表如下:
∴f(x)的单调递增区间是
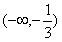 和(1,+∞);
和(1,+∞); f(x)的单调递减区间是
(3)函数g(x)=[f(x)-x3]·ex=(-x2-x+C)·ex,
有g'(x)=(-2x-1)ex+(-x2-x+C)ex
=(-x2-3x+C-1)ex,
当函数在区间x∈[-3,2]上为单调递增时,
等价于h(x)=-x2-3x+C-1≥0在x∈[-3,2]上恒成立,只要h(2)≥0,解得C≥11,
当函数在区间x∈[-3,2]上为单调递减时,等价于h(x)=-x2-3x+C-1≤0在x∈[-3,2]上恒成立,
即Δ=9+4(C-1)≤0,解得
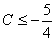
所以C的取值范围是C≥11或
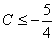 。
。 
练习册系列答案
相关题目