题目内容
已知向量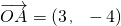 ,
,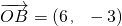 ,
, =(5-m,-3-m).
=(5-m,-3-m).
(1)若△ABC为直角三角形,且∠A为直角,求实数m的值;
(2)若点A,B,C能构成三角形,求实数m应满足的条件.
解:(1)因为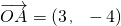 ,
,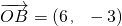 ,
,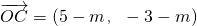 ,
,
所以 ,
, ,
,
若△ABC为直角三角形,且∠A为直角,则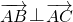 ,
,
∴3(2-m)+(1-m)=0,解得 .
.
(2)若点A,B,C能构成三角形,则这三点不共线,即 与
与 不共线,
不共线,
故知3(1-m)≠2-m,
∴实数 时,满足条件.
时,满足条件.
分析:(1)利用向量的运算法则求出 ,
, ;利用向量垂直的充要条件列出方程求出m.
;利用向量垂直的充要条件列出方程求出m.
(2)将构成三角形转化为三点不共线,利用向量共线的充要条件列出不等式求出m满足的条件.
点评:本题考查向量垂直的充要条件、向量共线的充要条件、利用向量共线解决三点共线问题、三点不共线问题.
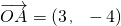 ,
,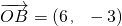 ,
,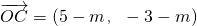 ,
,所以
 ,
, ,
,若△ABC为直角三角形,且∠A为直角,则
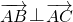 ,
,∴3(2-m)+(1-m)=0,解得
 .
.(2)若点A,B,C能构成三角形,则这三点不共线,即
 与
与 不共线,
不共线,故知3(1-m)≠2-m,
∴实数
 时,满足条件.
时,满足条件.分析:(1)利用向量的运算法则求出
 ,
, ;利用向量垂直的充要条件列出方程求出m.
;利用向量垂直的充要条件列出方程求出m.(2)将构成三角形转化为三点不共线,利用向量共线的充要条件列出不等式求出m满足的条件.
点评:本题考查向量垂直的充要条件、向量共线的充要条件、利用向量共线解决三点共线问题、三点不共线问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目