题目内容
已知函数f(x)=-x3+ax2+bx+c在(-∞,0)上是减函数,在(0,1)上是增函数,函数f(x)在R上有三个零点,且1是其中一个零点.
(1)求b的值 (2)求f(2)的取值范围
(1)0 (2)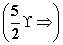
【解析】 (1)∵f(x)=-x3+ax2+bx+c,
∴f ′(x)=-3x2+2ax+b. …………3分
∵f(x)在(-∞,0)上是减函数,在(0,1)上是增函数,
∴当x=0时,f(x)取到极小值,即f ′(0)=0,
∴b=0.
(2)由(1)知,f(x)=-x3+ax2+c,
∵1是函数f(x)的一个零点,即f(1)=0,∴c=1-a.
∵f′(x)=-3x2+2ax=0的两个根分别为x1=0,x2=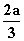 .
.
又∵f(x)在(-∞,0)上是减函数,在(0,1)上是增函数,且函数f(x)在R上有三个零点,
∴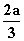 应是f(x)的一个极大值点,因此应有x2=
应是f(x)的一个极大值点,因此应有x2=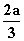 >1,即a>
>1,即a>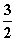 .
.
∴f(2)=-8+4a+(1-a)=3a-7>-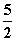 .
.
故f(2)的取值范围为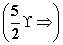 .
.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 内投点,点落在区域的每个位置是等可能的,则坐标原点与该点连线的倾斜角小于
内投点,点落在区域的每个位置是等可能的,则坐标原点与该点连线的倾斜角小于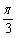 的概率为 。
的概率为 。 =
= 上是减函数,则
上是减函数,则 的取值范围是 。
的取值范围是 。 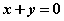 , 则
, 则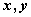 互为相反数”的逆命题;
互为相反数”的逆命题; 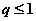 ,则
,则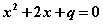 有实根”的逆否命题;
有实根”的逆否命题;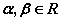 ,使
,使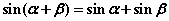 成立”的否定.
成立”的否定.
 的解所在的区间是( )
的解所在的区间是( ) B.
B.  C.
C. D.
D. 
 的周长是6,中心角是1弧度,则该扇形的面积为________.
的周长是6,中心角是1弧度,则该扇形的面积为________.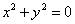 ,则x,y全为0”的逆命题;
,则x,y全为0”的逆命题;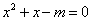 有实根”的逆否命题;
有实根”的逆否命题;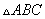 中,
中, 、
、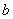 、
、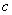 分别是角A、B、C所对的边长,若
分别是角A、B、C所对的边长,若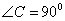 ,则
,则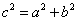 ”的逆否命题。
”的逆否命题。 的零点所在的大致区间是( )(参考数据
的零点所在的大致区间是( )(参考数据 ,
,
 )
) B
B C
C D
D