题目内容
【题目】已知数列![]() 满足
满足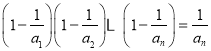 ,
,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)已知数列![]() 的通项公式为
的通项公式为![]() ,若对于一切
,若对于一切![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
(3)设![]() ,是否存在正整数
,是否存在正整数![]() ,使得数列
,使得数列![]() 中存在某项
中存在某项![]() 满足
满足![]() 成等差数列?若存在,求出符合题意的
成等差数列?若存在,求出符合题意的![]() 的集合;若不存在,请说明理由.
的集合;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]() 的集合为
的集合为![]() ,4,6,10,18,
,4,6,10,18,![]()
【解析】
(1)求得数列的首项,再将![]() 换为
换为![]() ,两式相除,化简,结合等差数列的定义和通项公式,可得所求;
,两式相除,化简,结合等差数列的定义和通项公式,可得所求;
(2)求得![]() ,运用作差判断数列的单调性,可得最小值,结合不等式恒成立问题解法,可得
,运用作差判断数列的单调性,可得最小值,结合不等式恒成立问题解法,可得![]() ,由对数函数的单调性可得所求
,由对数函数的单调性可得所求![]() 的范围;
的范围;
(3)求得![]() ,假设存在正整数
,假设存在正整数![]() ,使得数列
,使得数列![]() 中存在
中存在![]() 满足,
满足,![]() ,
,![]() ,
,![]() 成等差数列,运用等差数列的中项性质和整除的性质,可判断存在性.
成等差数列,运用等差数列的中项性质和整除的性质,可判断存在性.
(1)数列![]() 满足
满足![]() ,
,
可得![]() 时,
时,![]() ,即
,即![]() ,
,
![]() 时,
时,![]() ,又
,又![]() ,
,
两式相除可得![]() ,化为
,化为![]() ,
,
即数列![]() 为首项为2,公差为1的等差数列,可得
为首项为2,公差为1的等差数列,可得![]() ;
;
(2)![]() ,
,![]() ,
,
设![]() ,
,
![]() ,
,
可得![]() ,
,
则数列![]() 为递增数列,
为递增数列,![]() 的最小值为
的最小值为![]() ,
,
对于一切![]() ,不等式
,不等式![]() 恒成立,
恒成立,
可得![]() ,即有
,即有![]() 或
或![]()
解得:![]() ;
;
(3)设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
假设存在正整数![]() ,使得数列
,使得数列![]() 中存在
中存在![]() 满足,
满足,![]() ,
,![]() ,
,![]() 成等差数列,
成等差数列,
可得![]() ,即
,即![]() ,
,
当![]() 时,
时,![]() 无解;当
无解;当![]() 时,
时,![]() ,
,
又![]() 为正整数,
为正整数,![]() 为不小于6的正整数,可得
为不小于6的正整数,可得![]() ,2,4,8,16,32,
,2,4,8,16,32,
即![]() ,25,17,13,11,10,满足题意,
,25,17,13,11,10,满足题意,
故存在正整数![]() ,使得数列
,使得数列![]() 中存在
中存在![]() 满足,
满足,![]() ,
,![]() ,
,![]() 成等差数列,
成等差数列,
且![]() 的集合为
的集合为![]() ,4,6,10,18,
,4,6,10,18,![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】在某外国语学校举行的![]() (高中生数学建模大赛)中,参与大赛的女生与男生人数之比为
(高中生数学建模大赛)中,参与大赛的女生与男生人数之比为![]() ,且成绩分布在
,且成绩分布在![]() ,分数在
,分数在![]() 以上(含
以上(含![]() )的同学获奖.按女生、男生用分层抽样的方法抽取
)的同学获奖.按女生、男生用分层抽样的方法抽取![]() 人的成绩作为样本,得到成绩的频率分布直方图如图所示.
人的成绩作为样本,得到成绩的频率分布直方图如图所示.
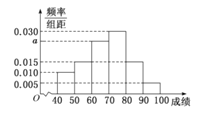
(Ⅰ)求![]() 的值,并计算所抽取样本的平均值
的值,并计算所抽取样本的平均值![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(Ⅱ)填写下面的![]() 列联表,并判断在犯错误的概率不超过
列联表,并判断在犯错误的概率不超过![]() 的前提下能否认为“获奖与女生、男生有关”.
的前提下能否认为“获奖与女生、男生有关”.
女生 | 男生 | 总计 | |
获奖 |
| ||
不获奖 | |||
总计 |
| ||
附表及公式:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中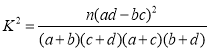 ,
,![]() .
.
【题目】大荔县某高中一社团为调查学生学习围棋的情况,随机抽取了![]() 名学生进行调查.根据调查结果绘制的学生均学习围棋时间的频率分布直方图.将日均学习围棋时不低于
名学生进行调查.根据调查结果绘制的学生均学习围棋时间的频率分布直方图.将日均学习围棋时不低于![]() 分钟的学生称为“围棋迷”.
分钟的学生称为“围棋迷”.
非围棋迷 | 围棋迷 | 合计 | |
男 | |||
女 |
|
| |
合计 |

(1)根据已知条件完成下面的![]() 列联表,并据此资料你是否有
列联表,并据此资料你是否有![]() 的把握认为“围棋迷”与性别有关?
的把握认为“围棋迷”与性别有关?
(2)现在从参与本次抽样调查的![]() 名学生的男同学里面,依据是否为围棋迷,采用分层抽样的方法抽取
名学生的男同学里面,依据是否为围棋迷,采用分层抽样的方法抽取![]() 名学生参与围棋知识竞赛,再从
名学生参与围棋知识竞赛,再从![]() 人中任选
人中任选![]() 人参与知识竞赛的赛前保障工作.求选到的
人参与知识竞赛的赛前保障工作.求选到的![]() 人恰好是一个“围棋迷”和一个“非围棋迷”的概率?
人恰好是一个“围棋迷”和一个“非围棋迷”的概率?
附:![]() ,
,
|
|
|
|
|
|
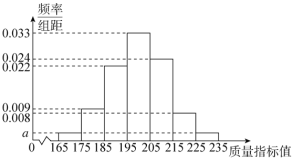
【题目】2019年下半年以来,各地区陆续出台了“垃圾分类”的相关管理条例,实行“垃圾分类”能最大限度地减少垃圾处置量,实现垃圾资源利用,改善生存环境质量.某部门在某小区年龄处于区间![]() 内的人中随机抽取
内的人中随机抽取![]() 人进行了“垃圾分类”相关知识掌握和实施情况的调查,并把达到“垃圾分类”标准的人称为“环保族”,得到图各年龄段人数的频率分布直方图和表中统计数据.
人进行了“垃圾分类”相关知识掌握和实施情况的调查,并把达到“垃圾分类”标准的人称为“环保族”,得到图各年龄段人数的频率分布直方图和表中统计数据.
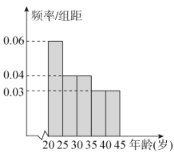
(1)求![]() 的值;
的值;
(2)根据频率分布直方图,估计这![]() 人年龄的平均值(同一组数据用该组区间的中点值代替,结果保留整数);
人年龄的平均值(同一组数据用该组区间的中点值代替,结果保留整数);
(3)从年龄段在![]() 的“环保族”中采用分层抽样的方法抽取9人进行专访,并在这9人中选取2人作为记录员,求选取的2名记录员中至少有一人年龄在区间
的“环保族”中采用分层抽样的方法抽取9人进行专访,并在这9人中选取2人作为记录员,求选取的2名记录员中至少有一人年龄在区间![]() 中的概率.
中的概率.
组数 | 分组 | “环保族”人数 | 占本组频率 |
第一组 |
| 45 | 0.75 |
第二组 |
| 25 |
|
第三组 |
|
| 0.5 |
第四组 |
| 3 | 0.2 |
第五组 |
| 3 | 0.1 |