题目内容
已知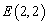 是抛物线
是抛物线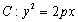 上一点,经过点
上一点,经过点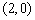 的直线
的直线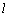 与抛物线
与抛物线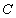 交于
交于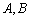 两点(不同于点
两点(不同于点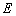 ),直线
),直线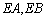 分别交直线
分别交直线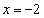 于点
于点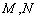 .
.
(Ⅰ)求抛物线方程及其焦点坐标;
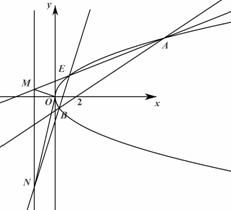
(Ⅱ)已知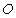 为原点,求证:
为原点,求证: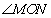 为定值并求出这个定值.
为定值并求出这个定值.
(Ⅰ)将 代入
代入 ,得
,得 ,所以抛物线方程为
,所以抛物线方程为 ,
,
焦点坐标为 2分
2分
(Ⅱ)因为直线 不经过点
不经过点 ,所以直线
,所以直线 一定有斜率设直线
一定有斜率设直线 方程为
方程为 ,与抛物线方程联立得到
,与抛物线方程联立得到 ,
,
消去 ,得:
,得: ,
,
则由韦达定理得: ,
,
直线 的方程为:
的方程为: ,即
,即 ,
,
令 ,得
,得 ,
,
同理可得: ,
,
又  ,
,



 。所以
。所以 ,即
,即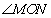 为定值
为定值 。 10分
。 10分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 后得到△A2B2C2.求B1变化后的对应点B2的坐标.
后得到△A2B2C2.求B1变化后的对应点B2的坐标. ,则
,则 取得
取得 极值时的x值为 .
极值时的x值为 .  中,
中, ,
, ,D是BC的中点,则
,D是BC的中点,则 ( )
( )
 的两根为
的两根为 ,且
,且 ,则
,则 .
.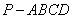 的底面边长为6cm,侧棱长为5cm,则它的正视图的面积等于
的底面边长为6cm,侧棱长为5cm,则它的正视图的面积等于 B.
B. 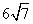 C.12 D.24
C.12 D.24

 表示的平面区域的面积为
表示的平面区域的面积为 ,则实数
,则实数 的值为
的值为 B.
B. D.
D.