题目内容
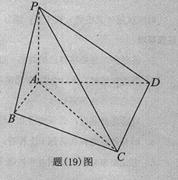
如题（19）图，四棱锥P－ ABCD中，PA⊥平面ABCD，AB∥CD，AB⊥AD，PA=CD=2AB=2，AD=3。
（I）证明：平面PCD⊥平面PAD；
（II）求棱锥A—PCD的高，
证明：（Ⅰ）因为
面
所以
又
所以
所以
面
又
面
所以面
面……………6分
（Ⅱ）由（Ⅰ）知
为直角三角形，
…8分
设
到面的距离为
，则由
得：
……………12分
练习册系列答案
高效智能课时作业系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
中，底面
为矩形，
底面
，
，点
在侧棱
上，
。 
证明：
求二面角
的大小。 
,AA1=2;点D在棱BB1上，BD＝
BB1；B1E⊥A1D，垂足为E，求： 
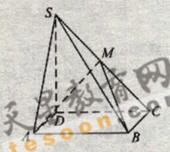
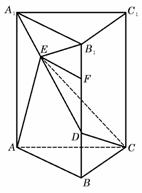
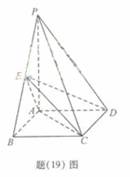如题（19）图，四棱锥P-ABCD中，底面ABCD为矩形，
底面ABCD，PA=AB=
，点E是棱PB的中点。
，求二面角A-EC-D的平面角的余弦值。
底面ABCD，PA=AB=
，点E是棱PB的中点。
，求二面角A-EC-D的平面角的余弦值。
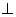底面ABCD，PA=AB=
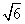，点E是棱PB的中点。
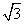，求二面角A-EC-D的平面角的余弦值。