题目内容
1．已知三棱锥P-ABC，若PA，PB，PC两两垂直，且PA=2，PB=PC=1，则三棱锥P-ABC的内切球半径为$\frac{1}{4}$．分析 利用三棱锥P-ABC的内切球的球心，将三棱锥分割成3个三棱锥，利用等体积，即可求得结论．
解答 解：由题意，设三棱锥P-ABC的内切球的半径为r，球心为O，则由等体积
VB-PAC=VO-PAB+VO-PAC+VO-ABC
可得$\frac{1}{3}×\frac{1}{2}×2×1×1$=$\frac{1}{3}×\frac{1}{2}×2×1×2×r$+$\frac{1}{3}×\frac{1}{2}×1×1×r$+$\frac{1}{3}×\frac{1}{2}×\sqrt{2}×\sqrt{5-\frac{1}{2}}×r$，
∴r=$\frac{1}{4}$．
故答案为：$\frac{1}{4}$．
点评 本题考查三棱锥P-ABC的内切球，考查学生分析转化问题的能力，正确求体积是关键．
练习册系列答案
相关题目
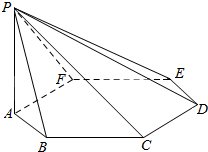设ABCDEF是边长为1的正六边形，PA垂直于正六边形所在的平面，且PA=2．求