观察等式sin20°+sin24°+sin20°•sin40°=$\frac{3}{4}$,sin228°+sin232°+sin28°•sin32°=$\frac{3}{4}$,请写出一个与以上两个等式规律相同的等式．题目和参考答案——青夏教育精英家教网—

题目内容

5．观察等式sin20°+sin24°+sin20°•sin40°=$\frac{3}{4}$；sin²28°+sin²32°+sin28°•sin32°=$\frac{3}{4}$；请写出一个与以上两个等式规律相同的等式．

分析根据角与角的关系，即可得出结论．

解答解：归纳有：sin²a+sin²（60-a）+sinasin（60-a）=$\frac{3}{4}$
证明如下：sin²60=sin²[a+（60-a）]=[sinacos（60-a）+cosasin（60-a）]²
=sin²acos²（60-a）+2sinasin（60-a）cosacos（60-a）+cos²asin²（60-a）
=sin²a[1-sin²（60-a）]+2sinasin（60-a）cosacos（60-a）+（1-sin²a]sin²（60-a）
=sin²a+sin²（60-a）]+2sinasin（60-a）[cosacos（60-a）-sinasin（60-a）]
=sin²a+sin²（60-a）]+2sinasin（60-a）[cosacos（60-a）-sinasin（60-a）]
=sin²a+sin²（60-a）]+2sinasin（60-a）cos60=sin²a+sin²（60-a）]+sinasin（60-a）=$\frac{3}{4}$．

点评本题考查归纳推理，考查学生分析解决问题的能力，分析左边角的规律是关键．

练习册系列答案

应用题天天练东北师范大学出版社系列答案

应用题天天练四川大学出版社系列答案

全国中考试题分类精选系列答案

初中学业考试指导系列答案

练习册吉林出版集团有限责任公司系列答案

16．已知向量$\overrightarrow a=（3，1）$，$\overrightarrow b=（1，3）$，$\overrightarrow c=（k，7）$，若$（\overrightarrow a-\overrightarrow c）$∥$\overrightarrow b$，则k=5．

13．直线y=x-4与抛物线y²=2x交于A，B两点，过A，B两点向抛物线的准线l作垂线，垂足分别为P，Q，则梯形APQB的面积为33．

20．如图程序运行结果是13，16．

10．已知x，y∈[0，2]，对于任意的m，n∈{1，2，3}，不等式$\sqrt{{x}^{2}+{y}^{2}}$＞|m-n|恒成立的概率为（　　）

17．已知函数y=f（x）的定义域为[0，+∞），且对于任意x₁，x₂∈[0，+∞），存在正实数L，使得|f（x₁）-f（x₂）|≤L|x₁-x₂|均成立．
（1）若f（x）=$\sqrt{1+x}$，x∈[0，+∞），求实数L的取值范围；
（2）当0＜L＜1时，正项数列{an}满足a_n+1=f（a_n），（n=1，2，…）
①求证：$\sum_{k=1}^{n}$|a_k-a_k+1|≤$\frac{1}{1-L}$•|a₁-a₂|；
②如果令A_k=$\frac{{a}_{1}+{a}_{2}+…+{a}_{n}}{k}$（k=1，2，3，…），
求证：$\sum_{k=1}^{n}$|A_k-A_k+1|≤$\frac{1}{1-L}$•|a₁-a₂|．

14．已知数列{b_n}是等比数列．
（1）若b₁=25，q=$\frac{1}{5}$，求b_n；
（2）若b₃=3，b₆=24，求q，b₁₀；
（3）若b₇=-$\frac{1}{8}$，b₂=-4，求b₁，b_n．

15．用集合表示终边在阴影部分的角a的集合为（　　）

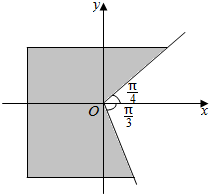
	A．	{a\|$\frac{π}{4}$≤a≤$\frac{π}{3}$}		B．	{a\|$\frac{π}{4}$≤a≤$\frac{5π}{3}$}
	C．	{a\|2kπ+$\frac{π}{4}$≤a≤2kπ+$\frac{π}{3}$，k∈Z}		D．	{a\|2kπ+$\frac{π}{4}$≤a≤2kπ+$\frac{5π}{3}$，k∈Z}