题目内容
已知椭圆
（
）的离心率
，直线
（
）与曲线
交于不同的两点
，
，以线段
为直径作圆
，圆心为。
（1）求椭圆的方程；
（2）若圆与
轴相交于不同的两点
，
，求
的面积的最大值。
（1）因为椭圆（）的离心率，所以
解得
。所以椭圆的方程为
。
（2）依题意，圆心为
（
）。
由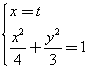
，得
。所以圆的半径为
。
因为圆与轴相交于不同的两点，，且圆心到轴的距离
，
所以
，即
。
则弦长
。…
所以的面积
…13分，当且仅当
，即
时，等号成立。所以的面积的最大值为
…
练习册系列答案
教学练新同步练习系列答案
课前课后同步练习系列答案
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案
相关题目
，它的离心率为
，直线
与以原点为圆心，以椭圆
的短半轴长为半径的圆相切.⑴求椭圆
，左准线为
，动直线
垂直于直线
，线段
的垂直平分线交
，求动点
的方程；⑶将曲线
,设曲线
，焦点为
，过
两点，过点
作平行于曲线
，若
，试证明三点
（
为坐标原点）在同一条直线上．
=1(
)的离心率为
,短轴一个端点到右焦点的距离为
.
的方程；
与椭圆
、
两点，坐标原点
到直线
，求△
面积的最大值.
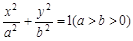的离心率与等轴双曲线的离心率互为倒数，直线
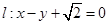与以原点为圆心，以椭圆C的短半轴长为半径的圆相切。
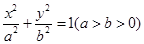的离心率为
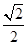，且经过点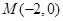
．
，
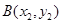两点，连接MA，MB并延长交直线x=4于P，Q两点，设yP，yQ分别为点P，Q的纵坐标，且
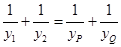．求△ABM的面积．