题目内容
已知椭圆非曲直的离心率为
,连接椭圆的四个顶点所得到的四边形的面积为2
,则椭圆的标准方程为
+y2=1
+y2=1.
| ||
| 2 |
| 2 |
| x2 |
| 2 |
| x2 |
| 2 |
分析:直接利用离心率为
,以及连接椭圆的四个顶点形成四边形的面积为2
列出关于a,b,c方程,求出a,b,c即可得到椭圆方程;
| ||
| 2 |
| 2 |
解答:解:由离心率 e=
,得 b=c=
a,又因为 2ab=2
,所以a=
,b=1,即椭圆标准方程为
+y2=1,
故答案为
+y2=1
| ||
| 2 |
| ||
| 2 |
| 2 |
| 2 |
| x2 |
| 2 |
故答案为
| x2 |
| 2 |
点评:本题主要考查椭圆的标准方程、几何性质,属于基础题.

练习册系列答案
相关题目

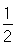

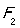

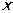
 ,连接椭圆的四个顶点所得到的四边形的面积为
,连接椭圆的四个顶点所得到的四边形的面积为 ,则椭圆的标准方程为 .
,则椭圆的标准方程为 .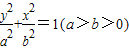 的离心率为
的离心率为 ,上、下顶点分别为A1,A2,椭圆上的点到上焦点F1的距离的最小值为1.
,上、下顶点分别为A1,A2,椭圆上的点到上焦点F1的距离的最小值为1.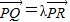 ,求λ的值.
,求λ的值.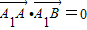 ,若存在,求出实数m的值;若不存在,请说明理由.
,若存在,求出实数m的值;若不存在,请说明理由.