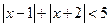题目内容
(本题满分10分)
设函数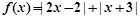 .
.
(1)解不等式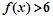 ;
;
(2)若关于的不等式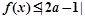 的解集不是空集,试求
的解集不是空集,试求 的取值范围.
的取值范围.
:(1)  ;(2)
;(2)  。
。
解析试题分析:(1)当x≥1时,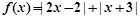 =3x+1>6,所以
=3x+1>6,所以 ;
;
当 时,
时,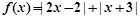 =2-2x+x+3=5-x>6,所以x<-1,所以-3≤x<-1;
=2-2x+x+3=5-x>6,所以x<-1,所以-3≤x<-1;
当x<-3时,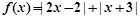 =2-2x-x-3=-3x-1>6,所以
=2-2x-x-3=-3x-1>6,所以 ,所以x<-3.
,所以x<-3.
综上知不等式的解集为  --------5分
--------5分
(2)  ,所以f(x)的最小值为4,所以要满足不等式
,所以f(x)的最小值为4,所以要满足不等式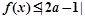 的解集不是空集,需
的解集不是空集,需 ,
,
所以实数a的取值范围为 --------5分
--------5分
考点:含绝对值不等式的解法;函数的最值。
点评:解含绝对值不等式的主要方法是:①利用“零点分段法”进行分段讨论,体想了分类讨论的数学思想。②利用绝对值不等式的几何意义来求解,体现了数形结合的思想。

练习册系列答案
相关题目
下列各式中,最小值等于2的是( )
A. | B. | C. | D. |
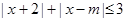 的解集为
的解集为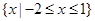 .
. 的值;
的值;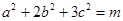 ,求
,求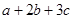 的取值范围.
的取值范围.
 ,集合B=
,集合B= 。
。 =2时,求
=2时,求 ;
; 时,求使
时,求使 的实数
的实数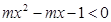 .
.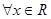 不等式恒成立,求实数
不等式恒成立,求实数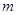 的取值范围;
的取值范围;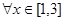 不等式恒成立,求实数
不等式恒成立,求实数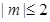 的一切m的值不等式恒成立,求实数
的一切m的值不等式恒成立,求实数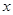 的取值范围.
的取值范围.
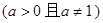 中的x的取值范围.
中的x的取值范围. 的不等式
的不等式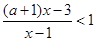 .
. 时,解该不等式;
时,解该不等式; 时,解该不等式.
时,解该不等式. 的一元二次不等式
的一元二次不等式
 时,求不等式
时,求不等式 取什么值时,关于
取什么值时,关于