��Ŀ����
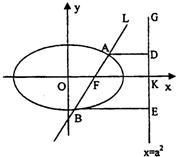 ��ͼ����ֱ֪��L��x=my+1����ԲC��
��ͼ����ֱ֪��L��x=my+1����ԲC��| x2 |
| a2 |
| y2 |
| b2 |
��1����֪������x2=4
| 3 |
������ԲC�ķ��̣�
����ֱ��L��y���ڵ�M����
| MA |
| AF |
| MB |
| BF |
��2������AE��BD����̽����m�仯ʱ��ֱ��AE��BD�Ƿ��ཻ��һ����N�������ڶ���N�������N������겢����֤��������˵�����ɣ�
��������1������������֪c=1��a2=b2+c2=4����ԲC�ķ���Ϊ
+
=1������l��y�ύ��M(0��-
)����A��x1��y1����B��x2��y2������
��֪��3m2+4��y2+6my-9=0����=144��m2+1����0��Ȼ���ɸ���ϵ���Ĺ�ϵ�������1+��2��ֵ��
��2����F��1��0����k=��a2��0������̽��m=0ʱ��ֱ��L��ox�ᣬ��ABED�ɶԳ���֪��AE��BD�ཻFK�е�N����N(
��0)���ٲ��룺��m�仯ʱ��AE��BD�ཻ�ڶ���N(
��0)��Ȼ�����������������֤����
| x2 |
| 4 |
| y2 |
| 3 |
| 1 |
| m |
|
��2����F��1��0����k=��a2��0������̽��m=0ʱ��ֱ��L��ox�ᣬ��ABED�ɶԳ���֪��AE��BD�ཻFK�е�N����N(
| a2+1 |
| 2 |
| a2+1 |
| 2 |
����⣺��1����֪b=
����b2=3����F��1��0������c=1��a2=b2+c2=4
����ԲC�ķ���Ϊ
+
=1��3�֣�
��l��y�ύ��M(0��-
)
��A��x1��y1����B��x2��y2������
�ࣨ3m2+4��y2+6my-9=0����=144��m2+1����0��
+
=
(*)��5�֣�
����
=��1
����(x1��y1+
)=��1(1-x1��-y1)
����1=-1-
ͬ����2=-1-
����1+��2=-2-
(
+
)=-2-
=-
��8�֣�
��3����F��1��0����k=��a2��0����
��̽������m=0ʱ��ֱ��L��ox�ᣬ��ABED�ɶԳ���֪��AE��BD�ཻFK�е�N����N(
��0)
���룺��m�仯ʱ��AE��BD�ཻ�ڶ���N(
��0)��9�֣�
֤������A��x1��y1����B��x2��y2����E��a2��y2����D��a2��y1��
��m�仯ʱ����AE������N
��
������a2+b2m2��y2+2mb2y+b2��1-a2��=0
�֡�=4a2b2��a2+m2b2-1����0��a��1��
��KAN=
��KEN=
��KAN-KEN=
(
(y1+y2)-my1y2=
•(-
)-m•
=
=0)
��KAN=KEN����A��N��E���㹲�ߣ�
ͬ���ɵ�B��N��D���㹲��
��AE��BD�ཻ�ڶ���N(
��0)��13�֣�
| 3 |
����ԲC�ķ���Ϊ
| x2 |
| 4 |
| y2 |
| 3 |
��l��y�ύ��M(0��-
| 1 |
| m |
��A��x1��y1����B��x2��y2������
|
�ࣨ3m2+4��y2+6my-9=0����=144��m2+1����0��
| 1 |
| y1 |
| 1 |
| y2 |
| 2m |
| 3 |
����
| MA |
| AF |
| 1 |
| m |
����1=-1-
| 1 |
| my1 |
| 1 |
| my2 |
����1+��2=-2-
| 1 |
| m |
| 1 |
| y1 |
| 1 |
| y2 |
| 2 |
| 3 |
| 8 |
| 3 |
��3����F��1��0����k=��a2��0����
��̽������m=0ʱ��ֱ��L��ox�ᣬ��ABED�ɶԳ���֪��AE��BD�ཻFK�е�N����N(
| a2+1 |
| 2 |
���룺��m�仯ʱ��AE��BD�ཻ�ڶ���N(
| a2+1 |
| 2 |
֤������A��x1��y1����B��x2��y2����E��a2��y2����D��a2��y1��
��m�仯ʱ����AE������N
��
|
�֡�=4a2b2��a2+m2b2-1����0��a��1��
��KAN=
| -y1 | ||
|
| -y2 | ||
|
��KAN-KEN=
| ||||
|
(
| a2-1 |
| 2 |
| a2-1 |
| 2 |
| 2mb2 |
| a2+m2b2 |
| b2(1-a2) |
| a2+m2b2 |
| (a2-1)•(mb2-mb2) |
| a2+m2b2 |
��KAN=KEN����A��N��E���㹲�ߣ�
ͬ���ɵ�B��N��D���㹲��
��AE��BD�ཻ�ڶ���N(
| a2+1 |
| 2 |
���������⿼��Բ���ߺ�ֱ�ߵ�λ�ù�ϵ���ۺ����ã�����ʱҪ�������⣬��ϸ���ע������ؽ��в��룮

��ϰ��ϵ�д�
�����Ŀ
 ��ͼ����ֱ֪��l��x=my+1����Բ
��ͼ����ֱ֪��l��x=my+1����Բ ��ͼ����ֱ֪��l��x=my+4��m��R����x�ύ�ڵ�P����������y2=2ax��a��0����A��B���㣬����ԭ��O��PQ���е㣬��ֱ��AQ��BQ��б�ʷֱ�Ϊk1��k2��
��ͼ����ֱ֪��l��x=my+4��m��R����x�ύ�ڵ�P����������y2=2ax��a��0����A��B���㣬����ԭ��O��PQ���е㣬��ֱ��AQ��BQ��б�ʷֱ�Ϊk1��k2�� ��ͼ����ֱ֪��L��x=my+1����ԲC��
��ͼ����ֱ֪��L��x=my+1����ԲC�� ��2012•��ɽ��ģ����ͼ����ֱ֪��L��x=my+1����ԲC��
��2012•��ɽ��ģ����ͼ����ֱ֪��L��x=my+1����ԲC��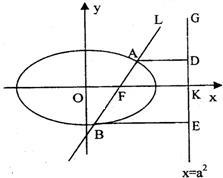 ��ͼ����ֱ֪��L��
��ͼ����ֱ֪��L��