题目内容
已知函数f(x)=2sin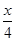 cos
cos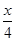 +
+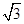 cos
cos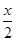 .
.
(1)求函数f(x)的最小正周期及最值;
(2)令g(x)=f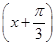 ,判断函数g(x)的奇偶性,并说明理由.
,判断函数g(x)的奇偶性,并说明理由.
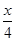 cos
cos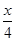 +
+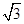 cos
cos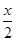 .
.(1)求函数f(x)的最小正周期及最值;
(2)令g(x)=f
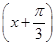 ,判断函数g(x)的奇偶性,并说明理由.
,判断函数g(x)的奇偶性,并说明理由.(1) 最小正周期4 ;(2) 函数g(x)是偶函数.
;(2) 函数g(x)是偶函数.
 ;(2) 函数g(x)是偶函数.
;(2) 函数g(x)是偶函数.试题分析:(1)利用两角和的正弦函数化简函数为一个角的一个三角函数的形式,然后直接求f(x)的最小正周期;(2)求出g(x)=f
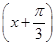 的表达式,通过函数的奇偶性的定义,直接证明即可.
的表达式,通过函数的奇偶性的定义,直接证明即可.试题解析:
 2分
2分∴f(x)的最小正周期T=
 =4
=4 .1分
.1分当
 时,f(x)取得最小值-2; 1分
时,f(x)取得最小值-2; 1分当
 时,f(x)取得最大值2 .1分
时,f(x)取得最大值2 .1分(2)g(x)是偶函数.理由如下: .1分
由(1)知
 ,又g(x)
,又g(x)
∴g(x)=
 3..分
3..分∵g(-x)=
 =g(x), .2分
=g(x), .2分∴函数g(x)是偶函数 ..1分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
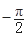 <j<0)图象上的任意两点,且角j的终边经过点P(l,-
<j<0)图象上的任意两点,且角j的终边经过点P(l,-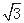 ),若|f(x1)-f(x2)|=4时,|x1-x2|的最小值为
),若|f(x1)-f(x2)|=4时,|x1-x2|的最小值为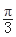 .
. 时,不等式mf(x)+2m≥f(x)恒成立,求实数m的取值范围.
时,不等式mf(x)+2m≥f(x)恒成立,求实数m的取值范围.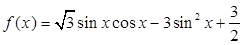 .
.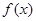 的最小正周期;
的最小正周期;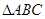 中,角
中,角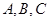 所对的边长分别为
所对的边长分别为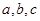 ,若
,若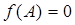 ,
,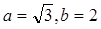 ,求
,求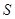 .
.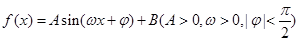 在某一
在某一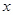














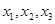 ,并直接写出函数
,并直接写出函数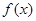 的解析式;
的解析式;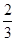 个单位得到函数
个单位得到函数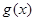 ,若函数
,若函数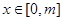 (其中
(其中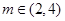 )上的值域为
)上的值域为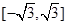 ,且此时其图象的最高点和最低点分别为
,且此时其图象的最高点和最低点分别为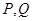 ,求
,求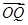 与
与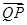 夹角
夹角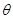 的大小.
的大小. , 则( ).
, 则( ). 两两为“同形”函数;
两两为“同形”函数; 为“同形”函数,且它们与
为“同形”函数,且它们与 不为“同形”函数;
不为“同形”函数; 为“同形”函数,且它们与
为“同形”函数,且它们与 不为“同形”函数.
不为“同形”函数. ;②
;② ;③
;③ ;④
;④ .则其中属于“互为生成函数”的是____________.
.则其中属于“互为生成函数”的是____________. 的部分图象如图所示,则
的部分图象如图所示,则 ( )
( )
 个单位后得到函数
个单位后得到函数 的图象,则
的图象,则 为 .
为 . 的图像关于直线
的图像关于直线 对称,且图像上相邻两个最高点的距离为
对称,且图像上相邻两个最高点的距离为 .
. 和
和 的值;
的值; ,求
,求 的值.
的值.