题目内容
【题目】如图,四边形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,
上, ![]() ,现将四边形
,现将四边形![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() .
.
(![]() )若
)若![]() ,是否存在折叠后的线段
,是否存在折叠后的线段![]() 上存在一点
上存在一点![]() ,且
,且![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(![]() )求三棱锥
)求三棱锥![]() 的体积的最大值,并求此时点
的体积的最大值,并求此时点![]() 到平面
到平面![]() 的距离.
的距离.

【答案】(1)答案见解析;(2)答案见解析.
【解析】试题分析:
(1)存在![]() ,使得
,使得![]() 平面
平面![]() ,此时
,此时![]() ,即
,即![]() ,利用几何关系可知四边形
,利用几何关系可知四边形![]() 为平行四边形,则
为平行四边形,则![]() ,利用线面平行的判断定理可知
,利用线面平行的判断定理可知![]() 平面
平面![]() 成立.
成立.
(2)由题意可得三棱锥![]() 的体积
的体积![]() ,由均值不等式的结论可知
,由均值不等式的结论可知![]() 时,三棱锥的体积
时,三棱锥的体积![]() 有最大值,最大值为
有最大值,最大值为![]() .
.
建立空间直角坐标系,则![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,故点
,故点![]() 到平面
到平面![]() 的距离
的距离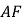 .
.
试题解析:
(![]() )存在
)存在![]() ,使得
,使得![]() 平面
平面![]() ,此时
,此时![]() .
.
证明:当![]() ,此时
,此时![]() ,
,
过![]() 作
作![]() ,与
,与![]() 交
交![]() ,则
,则![]() ,
,
又![]() ,故
,故![]() ,
,
∵![]() ,
, ![]() ,
,
∴![]() ,且
,且![]() ,故四边形
,故四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,
,
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() 成立.
成立.
(![]() )∵平面
)∵平面![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() ,
,
∴![]() ,
, ![]() ,
, ![]() ,
,
故三棱锥![]() 的体积
的体积![]() ,
,
∴![]() 时,三棱锥的体积
时,三棱锥的体积![]() 有最大值,最大值为
有最大值,最大值为![]() .
.
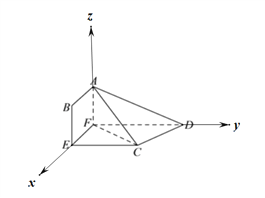
建立如图所示的空间直角坐标系,则![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
![]() ,
, ![]() ,
, ![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则![]() ,
,
∴![]() ,取
,取![]() ,则
,则![]() ,
, ![]() ,
,
∴![]() .
.
∴点![]() 到平面
到平面![]() 的距离
的距离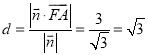 .
.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目